translated by Kynd
前章では、ニューラルネットワークが訓練を通じて、手書きの数字を90%程度というかなりの精度で識別できるようになる様子を見ました。この章ではネットワークの性能についてより丁寧に調べていきます。またその内部の状態を詳しく観察し、実際に何が起きているのかについて、いくつかの直感的な理解を得ます。章の後半では、より高いレベルへの到達にどんな種類のイノベーションが必要かを予測するため、イヌや自動車や船といった物のより複雑なデータセットを使って訓練を試み、ニューラルネットワークにあえて失敗をさせてみます。
重みを可視化する
MNISTの手書き文字を分類するよう訓練したネットワークを例にとってみましょう。前の章とは異なり、隠れ層を間に入れずに、入力層を直接出力層に繋げます。ネットワークは下の図のようになります。
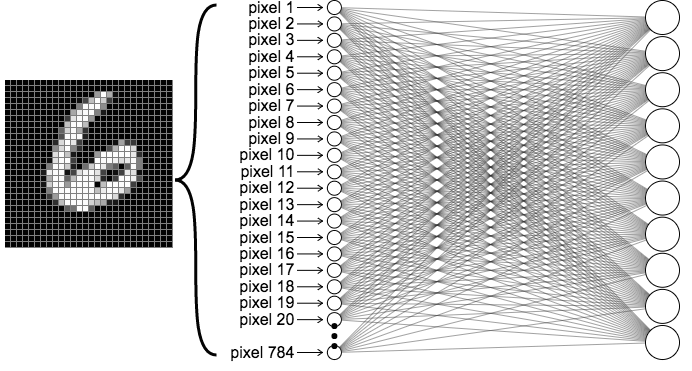
画像をニューラルネットワークに入力する際に、左下の画像のようにピクセルを一列に並べて可視化したことを思い出してください。最初の出力ニューロンへの繋がりだけに注目してみましょう。この出力ニューロンに\(z\)、それぞれの入力ニューロンとそれに対応する重みに\(x_i\)、\(w_i\)とラベルを付けます。

ピクセルを一列に並べる代わりに、対応するピクセルの位置に合わせて、28×28のグリッドに重み付けを並べてみましょう。右上の図と下の図は異なって見えますが、同じ等式、\(z=b+\sum{w x}\)を示しています。
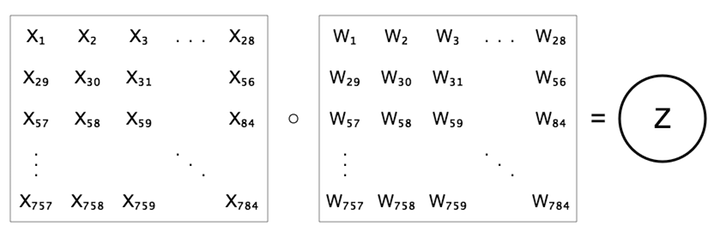
この構成で訓練したネットワークを例に、最初の出力ニューロンに流れ込む重みを可視化してみましょう。このニューロンの役割は数字の0を識別することです。重みが最も低いところが黒、最も高いところが白になるように色をつけます。

目を少し細めて見ましょう。ぼやけた0のように見えませんか。このように見える理由は、ニューロンが何をしているのかを考えるとより明確になります。このニューロンは0を識別する役割を担っているので、0に対して高い値を、それ以外に対して低い値を出力することをゴールとしています。0に対して高い値を出力するには、0の画像の中で明るくなることが多いピクセルに対して高い重みを割り当てます。また、0以外の数字に対して比較的低い値を出力するには、0以外の画像で明るいことが多く、0の画像で暗くなるピクセルに低い重みを割り当てます。重みの図の中心部分が暗くなっているのは、0の画像ではここがオフになることが多く(0の穴部分)、他の数字では大抵明るくなるからです。
10個の出力ニューロン全てについて、学習済みの重み付けを見てみましょう。予想通り、ややピンボケした10個の数字のように見えます。まるでそれぞれの数字に属する沢山の画像の平均を取ったかのようです。
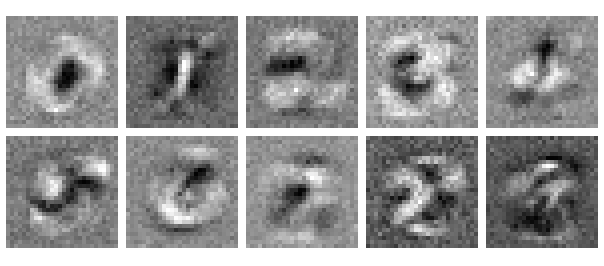
2の画像を受け取ったとします。2を識別する役割のニューロンは、2の画像で明るくなることの多いピクセルに高い値が対応するよう重み付けされているので、出力も大きくなるだろうと予測できます。他のニューロンでも、いくつかの重みは2の画像の明るいピクセルに対応した位置にあるので、多少スコアは高くなります。しかし2を識別するニューロンと比べると重なりは少なく、明るいピクセルの多くは低い重みづけによって打ち消されてしまいます。活性化関数は入力に対して単調増加、つまり入力が大きければ出力もより大きくなるので、結果としての順位に影響を与えることはありません。
訳注:最後の文がわかりにくいので補足。単調増加とは実数の値を持つ関数\(f\)について\(f(x)\leq f(y)\)であれば必ず\(f(x)\leq f(y)\)になることを言います。 前章で見た通り、それぞれのニューロンでは重みとバイアスを計算した後に活性化関数で出力を調整します。活性化関数が単調増加であれば、あってもなくても出力の大小関係には変化がありません。活性化関数なしの時点で2を判別するニューロンの出力が他のニューロンよりも大きければ、活性化関数を通しても結果は同じということです(厳密にいうとReLUは0以下の入力に対して必ず0を返すので、この範囲では全て引き分けになってしまいますが)。
重み付けは出力クラスの鋳型(テンプレート)だと考えることもできます。これはとても凄いことです。ネットワークは数字やその意味について、事前に全く何も教えられていないのにも関わらず、結果としてこれらのクラスに似たものを作り上げるのですから。これはネットワークの中で起きていることの何が本当に特別なのかを示唆しています。ニューロンは学習の対象についての表現を作り上げるのです。この表現は単純な分類や予想よりももっと高度なことに役立てられます。畳み込みニューラルネットワークについて学習する際には、この表現能力をより高いレベルに発展させます。でもまだ先回りはしないでおきましょう。
得られる答えよりも、より多くの疑問が湧いてきます。例えば、隠れ層を加えると重み付けには何が起きるのでしょう。すぐ後で触れますが、この疑問への答えは、前の節で直感的に確認したことの上に成り立ちます。しかしその前にニューラルネットワークの振る舞い、特にそれがどのような間違いを犯しやすいのかについて考えておくことが役立つでしょう。
0op5, 1 d14 17 2ga1n(おっとまた問偉えた)
ニューラルネットワークは時折、人間にも共感できる間違い方をします。私には下の図の最初の数字が9かどうかはっきりしません。ネットワークが間違えたのと同じく、4だと思う人も多いでしょう。同様に2つ目の数字の3が8に間違えられるのも理解できます。一方、3つ目、4つ目はもっと派手な間違いです。ほとんどの人は一目で3と2だと見分けられるでしょう。機械は前者を5と間違え、後者についてはほぼお手上げです。
訳注:この感覚は国や人によって大分違うと思います。日本人の多くは4つ目の例を2だとは思わないのではないでしょうか。

MNISTの数字に対して90%の精度を出した、前章のニューラルネットワークの動作をより詳しく見てみましょう。ネットワークの予測結果を表にした、混同行列を見るという方法があります。下に示す混同行列では、横の10行がMNISTデータセットの実際のラベルに相当し、縦の列がネットワークが予測したラベルに相当します。例えば4行6列目のマス目は、実際は3であるデータを、ニューラルネットワークが5だと間違えてラベル付けした例が71件あるということを示しています。混同行列の斜めの緑のマス目は正しい予測の回数、その他のマス目は間違いの回数を示しています。
マウスカーソルをマス目の上に載せると、それぞれのマス目の事例が、ネットワークが自信を持って予測した(正解である確率が高いと予測した)順に並んで表示されます。
下に示すように、混同行列のそれぞれのマス目にトップの事例を並べると、より良い洞察を得る事ができます。
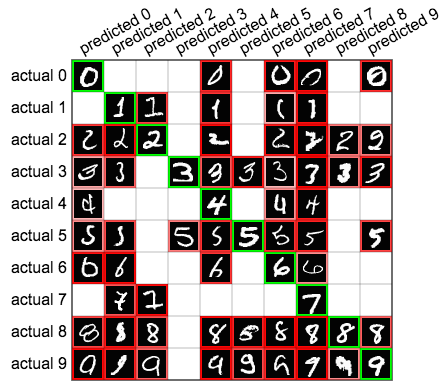
これを見るとネットワークが行う予測についての概観が得られます。最初の2列を見ると、ネットワークは、ゼロを予測するには大きな輪を、1を予測するには細い線を探していて、他の数字がこのような特徴を持っている場合に間違いを犯しているようだと見て取れます。
ネットワークに失敗させてみる
ここまでは、手書きの文字を識別するように訓練されたニューラルネットワークだけを見てきました。この例は多くの洞察を与えてくれますが、コンピュータにとても有利な、簡単すぎるデータセットでもあります。10個のはっきりしたクラスしかなく、各クラス内のデータには比較的わずかの違いしかありません。ほとんどの現実のシナリオでは、もっと理想とは遠いデータを分類することになります。同じニューラルネットワークの振る舞いを異なるデータセットを使って見てみましょう。CIFAR-10という、60000枚、32x32ピクセルの画像にラベルをつけたものを用います。画像は10種のクラス、飛行機、自動車、鳥、ネコ、シカ、イヌ、カエル、ウマ、船、トラックに分類されています。下図はCIFAR-10からランダムに選んだ例です。

これらの画像には、これまでに扱ったことのない違いがあると言わざるを得ないでしょう。例えばネコの画像は違う向きを向いていることもあれば、色や毛皮の模様が違うこともあり、伸びた姿勢をしていることや、丸まっていることもあれば、その他にも手書きの画像には見られなかったような様々な違いがあります。ネコの写真には他の物も散らばっていて、問題をより複雑にしています。
やはり、2層のニューラルネットワークをこれらの画像を使って訓練しても精度は37%しか出ません。それでもランダムよりはましですが(ランダムの場合は10%しか正解しない)、MNIST分類器の90%には遠く及びません。畳み込みネットワークを使うとMNISTとCIFAR-10の両方に対して数値を大きく改善できます。しかし今のところはまず、ネットワークの重み付けを調べることで通常のニューラルネットワークの欠点を正確に理解しましょう。
1層のみ、隠れ層なしのニューラルネットワークを使って先ほどと同じ重み付けを観察する実験を行いましょう。ただし今回はCIFAR-10の画像を使って訓練を行います。重み付けは下に示すようになります。

MNISTの重み付けと比較するとこれらには明確な特徴が少なく、輪郭もはるかに曖昧です。ディテールには直感的に納得できるものもあります。例えば飛行機と船は青空や水に囲まれていることが多いので、画像の輪郭付近が主に青色になっています。重み付けの画像はそのクラスに属する画像の平均と関連があるので、前回(訳注:MNIST判別器)と同じくぼんやりとした平均の色が見られると予測できます。しかしCIFARはクラスごとの一貫性がずっと低いので、MNISTで見られたようなはっきりしたテンプレートはなかなか現れません。
CIFAR分類器の混乱行列を見てみましょう。
やはり性能はとても低く37%にしかありません。単純な1層のニューラルネットワークでは明らかにこのデータセットの複雑さを扱うことができないのです。性能を幾らかでも改善する方法の1つは隠れ層を導入することです。次の節ではこの効果について分析します。
隠れ層を加える
これまでは入力が出力に直接繋がった1層のニューラルネットワークだけに注目してきました。隠れ層はニューラルネットワークにどのように影響を与えるのでしょうか。これは調べるために、MNISTネットワークに10個のニューロンから成る中間層を入れてみましょう。このニューラルネットワークは下の図のようになります。

784個の入力ピクセルはもはや出力クラスに直接繋がってはいないので、1層のネットワークで使った単純なテンプレートの例えはうまく当てはまりません。ある意味、1層のネットワークでは、それぞれの重みが1つのクラスにだけに繋がり影響するようにすることで、無理やりテンプレートを学ばせていたと言えるでしょう。しかし今回導入したようなより複雑なネットワークでは、隠れ層の重み付けは出力層の10個全てのニューロンに影響します。この場合の重み付けはどのように見えるでしょうか。
何が起きているか理解するために、前回同様、最初のレイヤーの重み付けを可視化します。今回はまた2層目で、これらのニューロンの活性化がどのように組み合わせられて各クラスのスコアを出力するのかについても注意深く見ることにします。ある画像が1層目の特定のニューロン(フィルター)とよく適合する場合に、そのニューロンは強く活性化します。10個のニューロンは元の画像に、異なる10種類の特徴がどれだけ強く現れているかを示します。出力レイヤーでは、クラスのラベルに相当するニューロンが、前の隠れ層の10個のニューロンの活性化を重み付けして組み合わせます。下の図を見てみましょう。
訳注:フィルターという表現が突然出てきました。ここではニューロンとその重み付けのことを指している、くらいの理解で良いと思います。誰か上手に説明できる人がいればお願いします。
画像の一番上に示された、1層目の10個の重み付けから始めましょう。もはやこれらは画像クラスのテンプレートのようには見えず、もっと見慣れない形をしています。いくつかは数字もどきのように、他のものは輪の半分、斜めの線、穴など数字の部品のように見えます。
フィルターの画像の下の行は、それぞれの画像クラスの出力ニューロンに対応します。棒グラフは隠れ層の10個のフィルターそれぞれのに対しての重み付けを示しています。例えば0のクラスは、(0の画像が現れることの多い)外側の淵に沿って高い値を示すフィルターを好んでいるように見えます。(0の画像では穴になることが多い)中央部分に高い値をもつフィルターは嫌われています。1のクラスはほとんどこの逆で、1の縦棒が描かれることが多い中央に高い値をもつフィルターを好んでいます。
このアプローチの利点はその柔軟性にあります。それぞれのクラスに対して、出力ニューロンを刺激するもっと多くの入力パターンがあります。クラスは、隠れ層でいくつかの抽象的な特徴やその組み合わせが見つかるかどうかに応じて発火します。つまり、色々な種類の0、色々な種類の1、といったように学習できるのです。このことは大抵 − 必ずではないですが − 概ねのタスクについてのネットワークの性能を改善します。
特徴と表現
この章で学んだことのいくつかを一般化してみましょう。1層、または複数のニューラルネットワークでは、それぞれの層は似通った機能を果たします。レイヤーは前のレイヤーからのデータをより「高レベルの」表現に変形します。「高レベル」とは、例えば要約が本の高レベルな表現であるように、そのデータをよりコンパクトかつ際立った形で表していることを意味します。例えば上の2層のネットワークでは、1層目で「低レベル」のピクセルを、数字の中に見つかる線、輪といったより「高レベル」な特徴に対応づけ、次のレイヤーでこれらの高レベルな特徴をさらに高レベルな表現、つまり実際の数字に対応づけました。この、データをより小さくもっと意味のある情報に変形するという概念こそが、機械学習の要であり、ニューラルネットワークの最も重要な機能なのです。
隠れ層を加えると、ニューラルネットワークは複数の抽象レベルで特徴を学ぶ機会を得られます。最初の方の層では低レベルな特徴を、後の層では前の層の特徴を組み合わせることでより高レベルな特徴を表した、豊かなデータの表現が手に入るのです。
これまで見てきたように隠れ層は精度を改善できますが、それはある程度までに限られています。レイヤーを増やし続けてもすぐに精度は改善しなくなり、計算コストが上がってしまいます。ニューラルネットワークに、隠れ層を使ってあり得る画像クラス全てを覚えておくようにただお願いする、というわけには行かないのです。畳み込みネットワークを使うというもっと良い方法を、後の章で取り上げます。
もっと読む(英語)
次の章では
次の章では、ニューラルネットワークの訓練という、これまでごまかし続けてきた重要な話題について学びます。つまりニューラルネットワークを構築し、勾配降下法やバックプロパゲーションという手法を使ってデータの学習を行うプロセスについてです。単純な線形回帰から始めて、サンプルを使って学習を進め、研究者が取り扱わなくてはならない訓練の様々な側面を説明することで、知識を積み上げて行きます。