translated by Tibor Udvari
Près d’un siècle avant la conception des réseaux neuronaux, Ada Lovelace a décrit l’ambition de construire «l’analyse du système nerveux». Bien que les analogies spéculatives entre les cerveaux et les machines soient aussi anciennes que la philosophie de l’informatique elle-même, ce n’est que quand Charles Babbage, le professeur d’Ada, a proposé le moteur analytique que nous avons imaginés de “calculatrices” ayant des capacités cognitives humaines. Ada n’a pas pour voir son rêve de construire le moteur se concrétiser, car les ingénieurs de l’époque étaient incapables de construire les circuits complexes que nécessitaient ses schémas. Néanmoins, l’idée a été transmise au siècle suivant quand Alan Turing l’a cité comme l’inspiration pour le Jeu d’imitation, ce qui allait bientôt être appelé le «Test de Turing». Ses ruminations dans les limites du calcul ont incité le premier boom l’intelligence artificielle, préparant le terrain pour le premier âge d’or des réseaux de neurones.
La naissance et la renaissance des réseaux de neurones
La récente résurgence des réseaux de neurones est une histoire particulière. Intimement liés aux débuts de l’IA, les réseaux neuronaux ont été formalisés pour la première fois à la fin des années 1940 sous la forme de machines de type B de Turing, en s’appuyant sur des recherches antérieures sur plasticité neuronale par des neuroscientifiques et des psychologues cognitifs qui étudient le processus d’apprentissage chez les êtres humains. Alors que la mécanique du développement cérébral était découverte, les informaticiens ont expérimenté des versions idéalisées du potentiel d’action et de la rétropropagation neurale pour simuler ce processus dans des machines.
Aujourd’hui, la plupart des scientifiques déconseillent de prendre cette analogie trop au sérieux, car les réseaux neuronaux sont strictement conçus pour résoudre les problèmes d’apprentissage machine, plutôt que de représenter le cerveau précisément, alors qu’un domaine complètement différent, les neurosciences computationnelles ont relevé le défi de modéliser fidèlement le cerveau. Néanmoins, la métaphore de l’unité de base des réseaux de neurones le neurone biologique simplifié s’est maintenue au fil des décennies. La progression des neurones biologiques aux neurones artificiels peut être résumée par les figures suivantes.
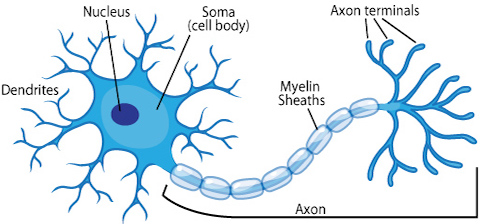
Source: ASU school of life sciences
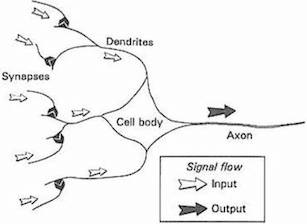
Source: Gurney, 1997. An Introduction to Neural Networks
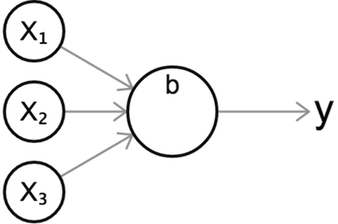
Les réseaux de neurones ont fait un grand pas en avant lorsque Frank Rosenblatt a conçu le Perceptron à la fin des années 1950, un type de classificateur linéaire que nous avons vu dans le dernier chapitre. Publiquement financé par la marine américaine, le perceptron Mark 1 a été conçu pour effectuer une reconnaissance d’image à partir d’un ensemble de photocellules, de potentiomètres et de moteurs électriques. Son efficacité à compléter des circuits électriques complexes a conduit le New York Times en 1958 à prédire qu’une machine allait bientôt «marcher, parler, voir, écrire, se reproduire et être consciente de son existence».
Le battage médiatique précoce inspirerait les écrivains de science-fiction pour les décennies à venir, mais l’excitation était beaucoup plus tempérée dans la communauté universitaire. Le livre de 1969 de Marvin Minsky et Seymour Papert, Perceptrons, a démontré diverses limitations - même triviales - conduisant par inadvertance à un déclin d’intérêt à la fois dans le milieu universitaire et dans le grand public, qui avait supposé par erreur que les ordinateurs suivraient simplement le rythme effréné du pouvoir de calcul. Même Turing lui-même a déclaré que les machines possédaient une intelligence de niveau humain d’ici 2000.
Malgré un certain nombre d’améliorations discrètes mais significatives apportées aux réseaux de neurones dans les années 80 et 90 [1][2][3], ils sont restés sur la touche jusqu’aux années 2000. La plupart des applications de l’apprentissage automatique les domaines commerciaux et industriels se sont concentrés sur les machines à vecteurs de supports et diverses autres approches. À partir de 2009 et surtout à partir de 2012, les réseaux neuronaux sont redevenus les algorithmes dominantes de l’apprentissage automatique. Leur résurgence a été largement provoquée par l’émergence des réseaux de neurones convolutifs et de réseaux de neurones récurrents, qui ont dépassé (parfois de manière dramatique) l’état de l’art des méthodes antérieures pour les problèmes clés dans le domaine audiovisuel. De plus, ils ont un certain nombre de nouvelles applications et propriétés inédites qui ont attiré l’attention des artistes et des autres en dehors du domaine de l’IA proprement dit. Ce livre examinera de plus près les réseaux de neurones convolutifs, dans un prochain chapitre dédié.
Bien que de nombreux algorithmes d’apprentissage aient été proposés au fil des années, nous concentrerons surtout notre attention sur les réseaux de neurones pour les raisons suivantes:
- Ils ont une formulation étonnamment simple et intuitive.
- Les réseaux neuronaux profonds sont l’état de l’art dans plusieurs problèmes d’apprentissage machine importantes, celles les plus pertinentes pour ce livre.
- La plupart des utilisations créatives récentes de l’apprentissage automatique ont été faites avec des réseaux de neurones.
De classificateurs linéaires aux neurones
Rappelez-vous du chapitre précédent que l’entrée d’un classificateur linéaire 2d ou régresseur a la forme:
\[\begin{eqnarray} f(x_1, x_2) = b + w_1 x_1 + w_2 x_2 \end{eqnarray}\]Plus généralement, dans un nombre quelconque de dimensions, il peut être exprimé comme
\[\begin{eqnarray} f(X) = b + \sum_i w_i x_i \end{eqnarray}\]Dans le cas de la régression, \(f(X)\) nous donne notre sortie prédite, étant donné le vecteur d’entrée \(X\). Dans le cas de la classification, notre classe prédite est donnée par
\[\begin{eqnarray} \mbox{classification} & = & \left\{ \begin{array}{ll} 1 & \mbox{if } f(X) \gt 0 \\ 0 & \mbox{if } f(X) \leq 0 \end{array} \right. \tag{1}\end{eqnarray}\]Chaque poids, \(w_i\), peut être interprété comme signifiant l’influence relative de l’entrée sur laquelle il est multiplié par \(x_i\). Le terme \(b\) dans l’équation est souvent appelé le biais, car il contrôle la façon dont le neurone est prédisposé à déclencher un 1 ou un 0, quel que soit le poids. Un biais élevée fait que le neurone nécessite une grande valeur en entrée pour produire un 1, un biais faible le permet plus facilement.
Nous pouvons passer de cette formule à un réseau de neurones en introduisant deux innovations. Le premier est l’ajout d’une fonction d’activation, qui transforme notre discriminateur linéaire en ce qu’on appelle un neurone, ou une « unité » (pour les dissocier de l’analogie cérébrale). La deuxième innovation est une architecture de neurones qui sont connectés séquentiellement en couches. Nous présenterons ces innovations dans cet ordre.
Fonction d’activation
Dans les réseaux de neurones artificiels et biologiques, un neurone ne sort pas seulement son entrée. Au lieu de cela, il y a une autre étape, appelée une fonction d’activation, analogue au taux de potentiel d’action tirant dans le cerveau. La fonction d’activation prend la même somme pondérée que précédemment, \(z = b + \sum_i w_i x_i\), puis la transforme une fois de plus avant de la sortir finalement.
De nombreuses fonctions d’activation ont été proposées, mais pour l’instant nous allons en décrire deux en détail: sigmoïde et ReLU.
Historiquement, la fonction sigmoïde est la fonction d’activation la plus ancienne et la plus populaire. Il est défini comme:
\[\sigma(x) = \frac{1}{1 + e^{-x}}\]\(e\) est la constante exponentielle, à peu près égale à 2,71828. Un neurone qui utilise un sigmoïde comme fonction d’activation est appelé un neurone sigmoïde. Nous fixons d’abord la variable \(z\) à la somme pondérée des entrées, puis la transmettons à la fonction sigmoïde.
\[z = b + \sum_i w_i x_i \\ \sigma(z) = \frac{1}{1 + e^{-z}}\]Au début, cette équation peut sembler compliquée et arbitraire, mais elle a en réalité une forme très simple, que nous pouvons visualiser si nous traçons la valeur de \(\sigma(z)\) en fonction de l’entrée \(z\).
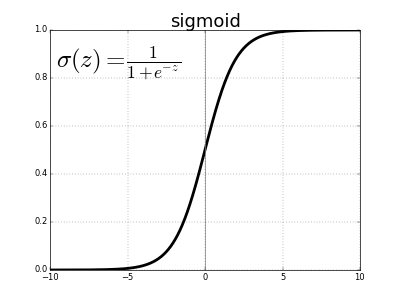
Nous pouvons voir que \(\sigma(z)\) agit comme une sorte de fonction de « écrasement », qui condense notre sortie précédente non bornée de 0 à 1. Au centre, où \(z = 0\), \(\sigma(0) = 1/(1+e^{0}) = 1/2\). Pour les grandes valeurs négatives de \(z\), le terme \(e^{-z}\) dans le dénominateur croît exponentiellement, et \(\sigma(z)\) se rapproche de 0. Inversement, les valeurs positives élevées de \(z\) rétrécit \(e^{-z}\) à 0, donc \(\sigma(z)\) se rapproche de 1.
La fonction sigmoïde est continuellement différentiable et sa dérivée est \(\sigma^\prime(z) = \sigma(z) (1-\sigma(z))\). C’est important parce que nous devons utiliser ce calcul pour entraîner les réseaux de neurones, mais ne vous en faites pas pour le moment.
Les neurones sigmoïdes ont été la base de la plupart des réseaux neuronaux pendant des décennies, mais ces dernières années ils sont devenus obsolètes. La raison de ceci sera expliquée plus en détail plus tard, mais en résumé, ils rendent difficiles les réseaux de neurones qui ont beaucoup de couches à former en raison du problème du gradient de fuite. Au lieu de cela, la plupart ont changé pour utiliser un autre type de fonction d’activation, l’unité linéaire rectifiée, ou ReLU. Malgré son nom obtus, il est simplement défini comme \(R(z) = max(0, z)\).
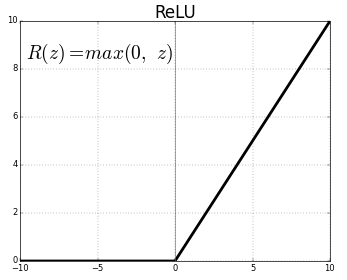
Autrement dit, les ReLUs laissent toutes les valeurs positives passer inchangées et attribuent simplement 0 aux valeurs négatives. Bien que les nouvelles fonctions d’activation gagnent du terrain, la plupart des réseaux neuronaux actuels utilisent ReLU ou l’une de ses variantes proches.
Quelle que soit la fonction d’activation utilisée, nous pouvons visualiser un seul neurone avec ce diagramme standard, ce qui nous donne une représentation visuelle intuitive du comportement d’un neurone.

Le diagramme ci-dessus montre un neurone avec trois entrées et une seule valeur de sortie \(y\). Comme avant, nous calculons d’abord la somme pondérée de ses entrées, puis la passons à travers une fonction d’activation \(\sigma\).
\[z = b + w_1 x_1 + w_2 x_2 + w_3 x_3 \\ y = \sigma(z)\]Vous vous demandez peut-être quel est le but d’une fonction d’activation et pourquoi il est préférable plutôt que de sortir simplement la somme pondérée, comme nous le faisons avec le classificateur linéaire du dernier chapitre. La raison en est que la somme pondérée \(z\) est linéaire par rapport à ses entrées, c’est-à-dire qu’elle a une dépendance plate sur chacune des entrées. En revanche, les fonctions d’activation non linéaires augmentent considérablement notre capacité à modéliser des fonctions curvées ou non triviales. Cela deviendra plus clair dans la section suivante.
Couches
Maintenant que nous avons décrit les neurones, nous pouvons maintenant définir les réseaux de neurones. Un réseau de neurones est composé d’une série de couches de neurones, de sorte que tous les neurones de chaque couche se connectent aux neurones de la couche suivante.
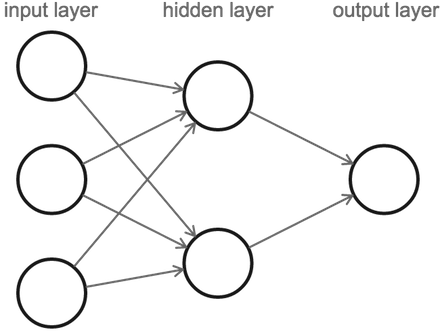
Notez que lorsque nous comptons le nombre de couches dans un réseau de neurones, nous ne comptons que les couches avec des connexions entrantes (en omettant notre première ou couche d’entrée). Donc, la figure ci-dessus est d’un réseau de neurones à 2 couches avec 1 couche cachée. Il contient 3 neurones d’entrée, 2 neurones dans sa couche cachée et 1 neurone de sortie.
Notre calcul commence avec la couche d’entrée sur la gauche, à partir de laquelle nous passons les valeurs à la couche cachée, puis à son tour, la couche cachée enverra ses valeurs de sortie à la dernière couche, qui contient notre valeur finale.
Notez qu’il peut sembler que les trois neurones d’entrée envoient des valeurs multiples parce que chacun d’eux est connecté aux deux neurones dans la couche cachée. Mais il n’y a vraiment qu’une seule valeur de sortie par neurone, elle est simplement copiée le long de chacune de ses connexions de sortie. Les neurones émettent toujours une valeur, quel que soit le nombre de neurones suivants.
Régression
Le processus d’un réseau de neurones envoyant une entrée initiale à travers ses couches vers la sortie est appelé propagation vers l’avant ou une passe avant et tout réseau de neurones qui fonctionne de cette manière est appelé un réseau de neurones feedforward. Comme nous le verrons bientôt, il existe des réseaux de neurones qui permettent aux données de circuler dans des cercles, mais ne nous laissons pas devancer …
Montrons une passe en avant avec cette démo interactive. Cliquez sur le bouton “Next” dans le coin supérieur droit pour continuer.
Plus de couches, plus d’expressivité
Pourquoi les calques cachés sont-ils utiles? Si nous n’avons pas de couches cachées et que nous faisions directement la correspondance des entrées à la sortie, la contribution de chaque entrée sur la sortie est indépendante des autres entrées. Dans les problèmes du monde réel, les variables d’entrée ont tendance à être fortement interdépendantes et elles affectent la sortie de manière combinatoire complexe. Les neurones de la couche cachée nous permettent de capturer des interactions subtiles entre nos entrées qui affectent la sortie finale sur la couche finale. Une autre façon d’interpréter cela est que les couches cachées représentent des « caractéristiques » de haut niveau ou des attributs de nos données. Chacun des neurones dans la couche cachée pèse les entrées différemment, en apprenant une caractéristique intermédiaire différente des données et notre neurone de sortie est alors une fonction de ceux-ci au lieu des entrées brutes. En incluant plus d’une couche cachée, nous donnons au réseau la possibilité d’apprendre plusieurs niveaux d’abstraction des données d’entrée originales avant d’arriver à une sortie finale. Cette notion de fonctionnalités de haut niveau deviendra plus concrète dans le chapitre suivant lorsque nous examinerons détaillement les couches cachées.
Rappelons-nous également que les fonctions d’activation élargissent notre capacité à capturer les relations non linéaires entre les entrées et les sorties. En enchaînant plusieurs transformations non linéaires à travers des couches, cela augmente considérablement la flexibilité et l’expressivité des réseaux de neurones. La preuve est complexe et dépasse la portée de ce livre, mais on peut même montrer que tout réseau de neurones à 2 couches avec une fonction d’activation non linéaire (incluant sigmoïde ou ReLU) et assez d’unités cachées est un approximateur de fonction universel, c’est-à-dire qu’il est théoriquement capable d’exprimer n’importe quel mappage arbitraire d’entrée à sortie. Cette propriété est ce qui rend les réseaux de neurones si puissants.
Classification
Et la classification? Dans le chapitre précédent, nous avons introduit la classification binaire en mettant un seuil de la sortie à 0; Si notre sortie était positive, nous la classerions positivement et si elle était négative, nous la classerions négativement. Pour les réseaux de neurones, il serait raisonnable d’adapter cette approche pour le neurone final et de le classer positivement si les scores de neurones de sortie sont au-dessus d’un certain seuil. Par exemple, nous pouvons mettre un seuil à 0,5 pour les neurones sigmoïdes qui sont toujours positifs.
Mais que faire si nous avons plusieurs classes? Une option pourrait être de créer des intervalles dans le neurone de sortie qui correspondent à chaque classe, mais cela serait problématique pour des raisons que nous verrons quand nous regardons comment les réseaux de neurones sont formés. Les réseaux de neurones sont adaptés pour la classification en ayant un neurone de sortie pour chaque classe. Nous faisons une passe avant et notre prédiction est la classe correspondant au neurone qui a reçu la valeur la plus élevée. Jetons un coup d’oeil à un exemple.
Classification des chiffres manuscrits
Intéressons-nous maintenant à un exemple réel de classification utilisant des réseaux de neurones, la tâche de reconnaître et d’étiqueter des images de chiffres manuscrits. Nous allons utiliser l’ensemble de données MNIST, qui contient 60,000 images étiquetées de chiffres manuscrits de 28 x 28 pixels, dont la précision de classification sert de référence dans la recherche d’apprentissage automatique. Voici un échantillon aléatoire d’images trouvées dans l’ensemble de données.

La façon dont nous configurons un réseau de neurones pour classer ces images est d’avoir les valeurs de pixels bruts comme première couche et ayant 10 classes de sortie, une pour chacune de nos classes numériques de 0 à 9. Comme ce sont des images en niveaux de gris, chaque pixel a une valeur de luminosité comprise entre 0 (noir) et 255 (blanc). Toutes les images MNIST sont 28x28, donc ils contiennent 784 pixels. Nous pouvons les dérouler en un seul tableau d’entrées, comme dans la figure suivante.

C’est important de se rendre compte que bien que ce réseau semble beaucoup plus imposant que notre simple réseau 3x2x1 dans le chapitre précédent, il fonctionne exactement comme avant, seulement avec beaucoup plus de neurones. Chaque neurone dans la première couche cachée reçoit toutes les entrées de la première couche. Pour la couche de sortie, nous aurons maintenant dix neurones plutôt qu’un seul, avec des connexions complètes entre elle et la couche cachée, comme avant. Chacun des dix neurones de sortie est affecté à l’étiquette d’une classe; le premier est pour le chiffre «0», le second pour «1» et ainsi de suite.
Après que le réseau de neurones a été formé - quelque chose dont nous parlerons plus en détail dans un chapitre futur - nous pouvons prédire le chiffre associé à des échantillons inconnus en les faisant passer par le même réseau et observer les valeurs de sortie. Le chiffre prédit est celui dont le neurone de sortie a la valeur la plus élevée à la fin. La démo suivante montre cela en action; cliquez sur “next” pour parcourir plus de prédictions.
Pour en savoir plus
Chapitre suivant
Dans le chapitre suivant, regardant dans les réseaux de neurones, nous analyserons de plus près les états internes des réseaux de neurones, construisant des intuitions sur les types d’informations qu’ils capturent, ainsi que les défauts des réseaux de neurones de base, en développant la motivation pour l’introduction de fonctionnalités plus complexes telles que les couches convolutives à explorer dans les chapitres suivants.