translated by Naoto Hieda
English 中文 español 한국어 français
ニューラルネットワークが発明される約一世紀前、エイダ・ラヴレスが「神経系の計算法」という野心的な提案をしました。脳と機械の推論的なアナロジーは計算自体の哲学と同じくらい古いものの、計算機が人間のような認知機能を持つことはエイダの師であるチャールズ・バベッジが解析機関を提案するまで考えられませんでした。当時の技術者たちは彼女の複雑な図面の回路を実現することができず、エイダは自身の夢である機関が完成するのを目の当たりにすることはできませんでした。しかしながらそのアイディアは次の世紀に継承され、アラン・チューリングにより後の「チューリング・テスト」であるイミテーション・ゲームのインスピレーションとして参照されました。チューリングの計算の極限への熟慮は第一次AIブームに火をつけ、ニューラルネットワークの第一次黄金時代への足掛かりとなりました。
ニューラルネットワークの誕生と復活
最近のニューラルネットワークの復活には奇妙な背景があります。 AIの初期に密接に関連していたニューラルネットワークは、ヒトの学習過程を研究する神経科学者と認知心理学者による神経可塑性の初期の研究に影響され、1940年代後半にチューリングの B-type machinesという形で最初に公式化されました。脳の発達のメカニズムが発見され、計算機科学者たちは活動電位と神経の逆伝播を定式化し、機械により脳のプロセスを再現しようと試みました。
今日ではニューラルネットワークは脳を正確に再現するのではなく機械学習により問題を解決する用途に限定して設計されているため、このアナロジーをあまり重視しないよう警鐘を鳴らしています。他方で計算論的神経科学は、脳を忠実にモデリングするという課題に取り組んできました。しかしながら、ニューラルネットワークは単純化された生物学的ニューロンであるという比喩は何十年にもわたって存在しています。 生物学的ニューロンから人工ニューロンへの進化を以下の図に要約しました。
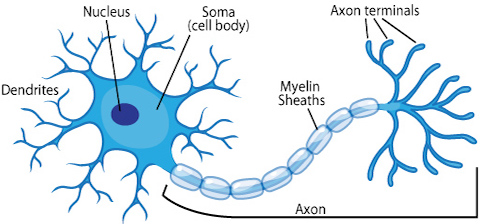
出展: ASU school of life sciences
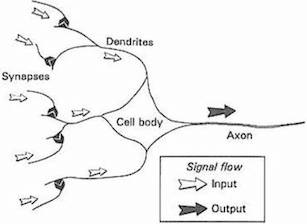
出展: Gurney, 1997. An Introduction to Neural Networks
ニューラルネットワークは、フランク・ローゼンブラットが1950年代後半にパーセプトロン(前章の線形分類器の一種)を考案したことにより大きく前進しました。米海軍の公的資金を受けて開発されたマーク1パーセプトロンは、複数のフォトセル、ポテンショメータ、およびモータを用いて画像認識を行うように設計されました。複雑な電気回路を完成させたことにより、1958年にニューヨーク・タイムズ紙はすぐにも機械が「歩く、話す、見る、書く、自らを複製し自分の存在を認知する」と予測しています。
このような初期の誇張された言説はサイエンスフィクション作家に何十年にもわたってインスピレーションを与えることになりましたが、その興奮は学界でははるかに落ち着いたものでした。人々はコンピュータがムーアの法則に乗っ取って異常なペースで計算能力が向上するだろうと楽観していましたが、マービン・ミンスキーとシーモア・パパートの1969年の本「パーセプトロンズ」が様々な、そして些細な制約を示したことで、意図せずにも学者と一般の両方の間で関心の低下を招きました。 チューリング自身でさえ、機械は2000年までに人間レベルの知性を持つだろうと言っていたのです。それは私たちが2000年問題に怯えていた年でした。
AIの冬の時代の80年代と90年代にはニューラルネットワークに数々の重要な改良がなされたにもかかわらず[1][2][3]、2000年代まで注目を浴びることはなく、機械学習の商業的および産業的応用の大部分にはサポートベクターマシンやその他の手法が用いられました。 2009年に始まり、特に2012年から顕著に、ニューラルネットワークは再び機械学習アルゴリズムの主要な手法となっています。その復活は、畳み込みとリカレントニューラルネットワークの発明に起因すると言っても過言ではなく、これまでの音声や画像解析の手法を劇的に上回るパフォーマンスを見せました。そして興味深いことに、以前は見られなかった多くの新しい応用や特徴があり、特にAI分野外のアーティストらの興味を惹きつけています。この本ではこれからいくつかの章にて、特に畳み込みニューラルネットワークについて詳しく見ていきます。
長年に渡って多くの学習アルゴリズムが提案されてきましたが、次の理由からここでは主にニューラルネットワークを取り扱います。
- 驚くほど簡単で直感的な定式化のため。
- ディープニューラルネットワークはいくつかの主要な機械学習の問題を解く上で現在の最先端技術であるため。
- 近年の機械学習のクリエイティブなアプリケーションのほとんどはニューラルネットワークで作られているため。
線形分類器からニューロンへ
前章で学んだ二次元線形分類器または線形回帰は次の式で表されます。
\[\begin{eqnarray} f(x_1, x_2) = b + w_1 x_1 + w_2 x_2 \end{eqnarray}\]一般的には任意の次元数において、
\[\begin{eqnarray} f(X) = b + \sum_i w_i x_i \end{eqnarray}\]となります。回帰の場合、\(f(X)\)は、説明変数であるベクトル\(X\)(入力)に対する目的変数(出力)となります。分類の場合、クラス確率は
\[\begin{eqnarray} \mbox{classification} & = & \left\{ \begin{array}{ll} 1 & \mbox{if } f(X) \gt 0 \\ 0 & \mbox{if } f(X) \leq 0 \end{array} \right. \tag{1}\end{eqnarray}\]です。それぞれのパラメータ\(w_i\)は、\(x_i\)と乗算した入力の相対的な影響を示すものとして解釈できます。方程式の\(b\)項はバイアス(切片)とよばれ、重みに関係なくニューロンが1または0を発火する要因となります。バイアスを高くすると、ニューロンが1を出力するためにより大きな入力を必要とし、低くするとより小さな入力が必要になります。
この式から本格的なニューラルネットワークにたどり着くためには二つのイノベーションが必要になります。一つ目は線形分類器をニューロンあるいはユニットに変える活性化関数です(ここで脳のアナロジーを排除するためにユニットという言葉を用いました)。二つ目は層状に接続されたニューロンの構造です。以下にこれらのイノベーションを紹介します。
Activation function
人工的および生物学的ニューラルネットワークの双方において、ニューロンは単に入力された情報に重み付けをして出力するわけではありません。脳内の活動電位の発火率に対応するように、活性化関数と呼ばれるステップがあります。活性化関数は、重み付き和\(z = b + \sum_i w_i x_i\)にもう一段階処理を施します。
多くの活性化関数が提案されていますが、ここではシグモイドとReLUについて説明します。
歴史的に、シグモイド関数は、最も古く普及した活性化関数で次のように定義されます。
\[\sigma(x) = \frac{1}{1 + e^{-x}}\]\(e\)はネイピア数を表し、おおよそ2.71828です。シグモイドを活性化関数に用いるニューロンをシグモイドニューロンと呼びます。まず先の重み付き和を変数\(z\)とし、それをシグモイド関数に渡します。
\[z = b + \sum_i w_i x_i \\ \sigma(z) = \frac{1}{1 + e^{-z}}\]この方程式は複雑で恣意的なものに見えるかもしれませんが、実際は非常に単純な形をしています。\(\sigma(z)\)の値を\(z\)の関数としてプロットしてみましょう。
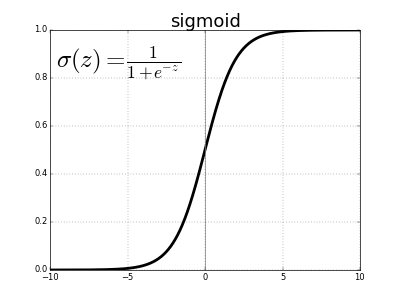
\(\sigma(z)\)は、任意の実数をとる先の重み付き和を0から1に制限する一種の「詰め込み」関数であることがわかります。また、中心では\(z = 0\)、\(\sigma(0) = 1/(1+e^{0}) = 1/2\)となります。\(z\)が大きな負の値の場合、分母の\(e^{-z}\)項は指数関数的に増加するため\(\sigma(z)\)は0に近づきます。逆に、\(z\)が大きな正の値をとると\(e^{-z}\)は0に近づき、\(\sigma(z)\)は1に近づきます。
シグモイド関数は連続的に微分可能であり、その導関数は便利なことに\(\sigma^\prime(z) = \sigma(z) (1-\sigma(z))\)です。ニューラルネットワークの学習には微積分が必要なため後に重要になりますが、ここでは心配する必要はありません。
シグモイドニューロンは、数十年にわたる大部分のニューラルネットワークの基礎となりましたが、近年では他の関数に興味が移っています。その理由は後ほど詳しく説明しますが、端的には勾配消失を招き多層ニューラルネットワークの学習が難しくなってしまうからです。そのためほとんどの場合、別のタイプの活性化関数、レクティファイドリニアユニット、略してReLUが使用されます。その堅苦しい名前にもかかわらず、それの定義は\(R(z) = max(0, z)\)とシンプルなものです。
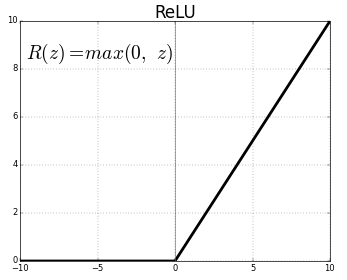
言い換えれば、ReLUは正の値をそのまま通しますが、負の値は0にとして出力します。新しい活性化関数も登場していますが、最近のほとんどの深層ニューラルネットワークでは、ReLUまたはその亜種が用いられます。
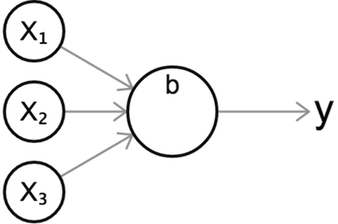
どの活性化関数を使用してもこの標準的な図で単一ニューロンを視覚化することができ、ニューロンの動作を直感的に視覚的に表現するのに役立ちます。

上の図のニューロンは3つの入力に対して\(y\)を出力します。これまでのように、まず入力の重み付き和を計算し、それを活性化関数\(\sigma\)に渡します。
\[z = b + w_1 x_1 + w_2 x_2 + w_3 x_3 \\ y = \sigma(z)\]前章の線形分類子と同様に、アクティベーション関数の目的や、なぜ重み付き和をそのまま出力するのか不思議に思えるかもしれません。その理由は、重み付き和\(z\)は、その入力に対して線型である、すなわち各入力に対して一次関数としての性質を持っているからです。対照的に、非線形活性化関数は、カーブを持つあるいはその他の複雑な関数をモデル化するのに役立ちます。これは次節でより明確になるでしょう。
レイヤー(層)
ここまでの知識に基づいてニューラルネットワークを定義することができます。ニューラルネットワークは、一つの層のすべてのニューロンが次の層のニューロンに接続するような一連のニューロンの層で構成されています。
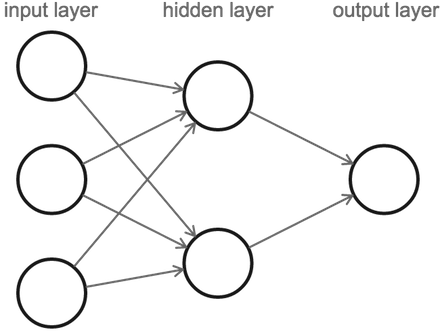
ここでニューラルネットワークの層の数を数えるとき、入力のある層の数だけがカウントされることに注意してください(最初の層、すなわち入力層は数えられません)。したがって上の図は、1つの隠れ層を持つ2層のニューラルネットワークです。詳しく見ると、3つの入力ニューロンと、隠れ層に2つのニューロン、1つの出力ニューロンで構成されています。
計算は次の順に行われます。左の入力層から開始し、そこから値を隠れ層に渡してから、隠れ層は最後の層に値を送り最終出力となります。
3つの入力ニューロンはそれぞれが隠れ層の両方のニューロンに接続されているため、複数の値を出力するように見えるかもしれません。しかし実際にはニューロンごとに1つの出力値しかなく、各出力先には同じ値が出力されます。つまりニューロンはいくつもの後続のニューロンに出力をしても、常に同じ値を出力するのです。
回帰
ニューラルネットワークが初期の入力を層ごとに処理して出力に向けて送ることをフォワードプロパゲーション(順伝搬)またはフォワードパスと呼び、このように動作するニューラルネットワークは一般にフィードフォワードニューラルネットワークと呼ばれます。以下で触れるように、データが環状に流れるようなニューラルネットワークもいくつかありますが、まだ気にする必要はありません。
次のインタラクティブなデモでフォワードパスについて詳しく見てみましょう。右上にある「次へ」ボタンをクリックしてください。
層を増やすことで表現力を高める
なぜ隠れ層が必要なのでしょうか。隠れ層がなく入力が出力に直接つながっている場合、入力変数同士が互いに干渉することはありません。現実の問題では入力変数間には強い相関があり、複雑に組み合いながら出力に影響を与えます。隠れ層のニューロンは、最終出力に影響を及ぼすであろう入力変数間の小さな相互作用を見つけることができます。 別の解釈として、隠れ層がデータの高次元の特徴や属性を表すことが挙げられます。隠れ層は入力されたデータのいくつかの中間特性をそれぞれのニューロンが学習してそれに応じて重みを設定し、最終出力のニューロンは入力変数の代わりに中間特性の関数になります。複数の隠れ層を用いることで、最終出力に達する前に元の入力データの複数の次元で抽象化を行い学習する機会をネットワークに与えます。この抽象化の概念については、次の章で隠れ層を詳しく見る中でより具体的に説明します。
また活性化関数は、入力と出力の間に非線形の関係もたらすことを思い出してください。複数の非線形変換を層ごとに連鎖させることにより、ニューラルネットワークの柔軟性と表現力が劇的に向上します。証明は複雑で本書の範囲を超えていますが、例えば非線形活性化関数(シグモイドやReLUを含む)と十分な数のニューロンを持つ2層ニューラルネットワークでさえ理論的には任意の入力と出力マッピングを表現することができます(汎関数近似)。この特徴のためニューラルネットワークは非常に強力になります。
分類
分類はどのように行うのでしょうか。前章では、単純に0を出力の閾値とした二値の分類を導入しました。出力が正の値なら正のクラスに分類し、負の値であれば負のクラスに分類します。ニューラルネットワークでは出力ニューロンの値がある閾値を上回った場合には正に分類するといったように、出力ニューロンの値にこの手法を用いることが妥当です。例えば、常に正を返すシグモイドニューロンの場合、閾値を0.5とすることが考えられます。
しかし、複数のクラスを用いる場合はどうでしょうか。一つの選択肢として各クラスに対応するように出力ニューロンに複数の閾値を設定することが考えられますが、ニューラルネットワークの訓練を見て明らかになるようにいくつかの問題が起きます。ニューラルネットワークは各クラスに対して1つの出力ニューロンを持つことで分類を可能にするためです。そこでフォワードパスを行い、最も高い値を出力したニューロンに対応するクラスを予測結果とします。それでは次の例を見てみましょう。
手書き数字の分類
ここでは手書き数字の画像を認識してラベル付けする例を用いて、ニューラルネットワークを使った実際の分類に取り組んでみましょう。ここで用いるMNISTデータセットは60,000枚の28×28ピクセルの手書き数字の画像から成り、機械学習の精度を評価するうえで共通のベンチマークとなっています。以下は、データセット内から無作為に取り上げた画像です。

これらの画像を分類するためには、ピクセルの値を最初の層の入力とし、0から9までの各桁に対応した10の出力クラスを持つようにニューラルネットワークを設定します。グレースケール画像であるため、それぞれのピクセルは輝度に対応して0(黒)〜255(白)の値を持ちます。全てのMNIST画像は28×28であるので、一つの画像につき784画素です。これを引き延ばすことで次の図のように、一次元の入力配列に展開することができます。

ここで気を付けたいのは、このネットワークは前章の単純な3x2x1ネットワークよりもはるかに仰々しく見えますが、ニューロンの数が多いだけで以前とまったく同じように動作します。第1の隠れ層の各ニューロンは、第1層からのすべてのニューロンの入力を受け取ります。出力層では、これまでのように1つだけでなく10個のニューロンを持ち、それぞれが隠れ層のすべてのニューロンに接続しています。1番目の出力ニューロンは数字の0、2番目の数字は1、となるように10個の出力ニューロンそれぞれが別々のクラスラベルに割り当てられています。
詳細については次章で説明しますが、ニューラルネットワークが訓練された後、未知の画像をネットワークに入力して出力値を処理することで画像にの表す数字を予測することができます。出力層の中で最大値を出力したニューロンに対応したラベルが予測された数字となります。次のデモではその動作を見ることができます。「次へ」をクリックすると、より多くの予測を見ることができます。
もっと読む(英語)
次の章では
次の章「ニューラルネットワークの中をのぞく」では、ニューラルネットワークの内部をより詳細に分析し、ニューラルネットワークがどのような情報を選りすぐっているのかについての簡単な理解をする他、 基本的なニューラルネットの問題点を見つけながら、後の章で説明する畳み込み層などのより複雑な機能を導入するきっかけを探します。