translated by Irene Alvarado
Casi un siglo antes de que las redes neuronales fueran primero concebidas, Ada Lovelace describió su ambición por construir un “cálculo del sistema nervioso.” Aunque la filosofía de la computación ha explorado analogías especulativas sobre mentes y máquinas desde hace mucho años, no fue hasta que el profesor de Ada, Charles Baggage, propuso la Máquina analítica que empezamos a concebir “calculadoras” teniendo capacidades cognitivas humanas. Ada no viviría para ver realizado su sueño de contruir una máquina similar a la que propuso Baggage, ya que los ingenieros de su época eran incapaces de producir los circuitos complejos que sus esquemas requerían. Sin embargo, la idea sobrevivió hasta el siguiente siglo cuando Alan Turing la citó como inspiración para el Juego de Imitación, lo cual pronto llegó a llamarse el “Test de Turing.” Sus reflexiones sobre los límites de la computación incitaron el primer auge en inteligencia artificial, la cual abrió paso para la primera época dorada de las redes neurales.
Nacimiento y renacimiento de redes neuronales
El resurgimiento reciente de las redes neuronales es una historia peculiar. Íntimamente conectadas a los primeros días de la inteligencia artificial, las redes neuronales se formalizaron a finales de los años 40 en la forma de máquinas tipo-B de Turing y estaban basadas en investigaciones de plasticidad neuronal conducidas por neurocientíficos y psicólogos cognitivos que estudiaban el proceso de aprendizaje en los seres humanos. A medida que se descubrió cómo se desarrolla el cerebro, los científicos de la computación comenzaron a experimentar con versiones idealizadas de acción potencial y retropropagación neural para simular el proceso en máquinas.
Hoy en día, la mayoría de los científicos nos advierten que deberíamos tener cuidado con esta analogía, ya que las redes neuronales fueron diseñadas para resolver problemas de aprendizaje de máquinas (en inglés, machine learning) y no para representar el cerebro con precisión. Sin embargo, la idea de que una neurona biológica simplificada representa la unidad central de una red neuronal es una metáfora que ha perdurado a través de las décadas. La progresión de las neuronas biológicas a las neuronas artificiales se puede resumir con la siguiente gráfica.
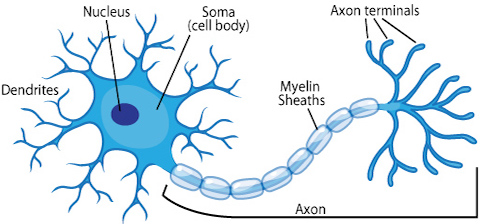
Source: ASU school of life sciences
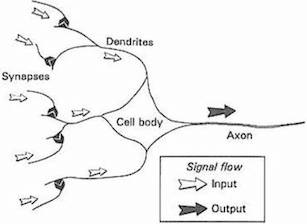
Source: Gurney, 1997. An Introduction to Neural Networks
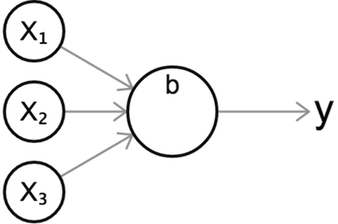
Las redes neuronales dieron un gran paso adelante cuando Frank Rosenblatt diseñó el Perceptron, un tipo de clasificador lineal que cubrimos en el capítulo anterior, a finales de los años cincuenta. Financiado públicamente por la Armada de los Estados Unidos, el perceptrón Mark 1 fue diseñado para reconocer imágenes a partir de una serie de fotocélulas, potenciómetros y motores eléctricos. Fue tan efectivo completando circuitos eléctricos complejos que en 1958 el periódico New York Times predijo que una máquina pronto podría “caminar, hablar, ver, escribir, reproducirse y ser consciente de su propia existencia”.
Este tipo de logros inspiró por décadas a escritores de ciencia ficción, aun cuando la emoción dentro de la comunidad académica fue mucho más reservada. En 1969 el libro de Marvin Minsky y Seymour Papert, Perceptrons, demostró varias limitaciones de las redes neuronales, lo cual condujo inadvertidamente a una disminución de interés por parte del mundo académico y el público general. Ambos habían asumido erróneamente que las computadoras seguirían avanzando al mismo ritmo vertiginoso que el poder computacional. Incluso Turing una vez dijo que las máquinas poseerían una inteligencia comparable a la humana para el año 2000 - el mismo año que tuvimos el susto Y2K.
A pesar de que las redes neuronales mejoraron de manera significativa en los años 80 y 90 [1][2][3], no fueron muy populares durante los años 2000, cuando la mayoría de las aplicaciones comerciales e industriales de aprendizaje de máquinas usaban técnicas como las máquinas de soporte vectorial. A partir del 2009 y sobre todo a partir del 2012, las redes neuronales volvieron a convertirse en la técnica dominante de muchos algoritmos de aprendizaje de máquinas. Su resurgimiento se debió en gran parte a la creación de las redes neuronales convolucionales y recurrentes, las cuales han resuelto problemas claves en el ámbito audiovisual mucho mejor que métodos antiguos. Lo más interesante es que estas redes neuronales tienen propiedades y aplicaciones completamente nuevas, lo cual ha cautivado el interés de artistas y profesionales fuera del campo de la inteligencia artifical. En este libro examinaremos en particular las redes neuronales convolucionales.
Aunque se han propuesto muchos algoritmos de aprendizaje automático a lo largo de los años, nos enfocaremos en la redes neuronales ya que:
- Tienen una formulación sorprendentemente simple e intuitiva.
- Las redes neuronales de aprendizaje profundo (en inglés, deep neural networks) constituyen la tecnología de vanguardia para varias de las tareas que discutiremos en este libro.
- La mayoría de las aplicaciones creativas del aprendizaje de máquinas se han hecho con redes neuronales.
De clasificadores lineales a neuronas
Recuerda que en el capítulo anterior discutimos que la entrada a un regresor o un clasificador lineal en 2d tiene la forma:
\[\begin{eqnarray} f(x_1, x_2) = b + w_1 x_1 + w_2 x_2 \end{eqnarray}\]Si lo extendemos a cualquier número de dimensiones, se puede expresar como:
\[\begin{eqnarray} f(X) = b + \sum_i w_i x_i \end{eqnarray}\]En el caso de la regresión, \(f(X)\) nos da el resultado predicho, dado el vector de entrada \(X\). En el caso de la clasificación, la clase predicha está dada por:
\[\begin{eqnarray} \mbox{classification} & = & \left\{ \begin{array}{ll} 1 & \mbox{if } f(X) \gt 0 \\ 0 & \mbox{if } f(X) \leq 0 \end{array} \right. \tag{1}\end{eqnarray}\]Podemos interpretar que cada peso, \(w_i\), representa la influencia relativa de la entrada por la cual se multiplica, \(x_i\). A menudo al término \(b\) se le llama sesgo (en inglés bias), ya que controla qué tan predispuesta está la neurona a disparar un 1 o un 0 independiente de los pesos. Un sesgo alto hace que la neurona requiera una entrada más alta para generar una salida de 1. Un sesgo bajo lo hace más fácil.
Podemos obtener una verdadera red neuronal a partir de esta fórmula si introducimos dos innovaciones. La primera es la adición de una función de activación, la cual transforma nuestro discirimador lineal en lo que se llama una neurona, o “unidad” (para disociarlo de analogías del cerebro). La segunda innovación consiste en organizar las neuronas de una manera particular: una arquitectura de neuronas conectadas secuencialmente en capas. Cubriremos estas dos innovaciones en orden.
Función de activación
Tanto en las redes neuronales artificiales como biológicas, una neurona no sólo transmite la entrada que recibe. Existe un paso adicional, una función de activación, que es análoga a la tasa de potencial de acción disparando en el cerebro. La función de activación utiliza la misma suma ponderada de la entrada anterior, \(z = b + \sum_i w_i x_i\), y la transforma una vez más como salida.
Se han propuesto muchas funciones de activación, pero por ahora describiremos solamente dos en detalle: la sigmoide y ReLU.
Históricamente, la función sigmoide es la función de activación más antigua y popular. Se define como:
\[\sigma(x) = \frac{1}{1 + e^{-x}}\]\(e\) denota la constante exponencial, que es aproximadamente igual a 2,71828. Una neurona que utiliza la sigmoide como función de activación se llama neurona sigmoide. Primero establecemos que la variable \(z\) equivale a nuestra suma ponderada de entrada y después la pasamos a través de la función sigmoide.
\[z = b + \sum_i w_i x_i \\ \sigma(z) = \frac{1}{1 + e^{-z}}\]Aunque la ecuación parece complicada y arbitraria, en realidad tiene una forma bastante simple. La podemos ver si trazamos el valor de \(\sigma(z)\) como función de la entrada \(z\).
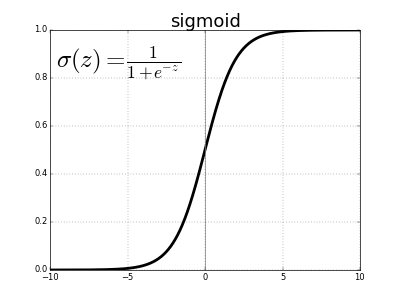
Podemos ver que \(\sigma(z)\) actúa como una especie de función “aplastadora”, comprimiendo nuestra salida a un rango de 0 a 1. En el centro, donde \(z = 0\), \(\sigma(0) = 1/(1+e^{0}) = 1/2\). Para valores negativos grandes de \(z\), el término \(e^{-z}\) en el denominador crece exponencialmente, y \(\sigma(z)\) se aproxima a 0. Al contrario, valores positivos grandes de \(z\) reducen \(e^{-z}\) hacia 0, y \(\sigma(z)\) se aproxima a 1.
La función sigmoide es continuamente diferenciable, y su derivada convenientemente es \(\sigma^\prime(z) = \sigma(z) (1-\sigma(z))\). Este detalle indica que tenemos que usar cálculo para entrenar una red neuronal – pero no nos preocuparemos por eso en este capítulo.
Las funciones sigmoides fueron la base de la mayoría de las redes neuronales por muchas décadas, aunque en años recientes han perdido popularidad. Explicaremos la razón en detalle en los próximos capítulos, pero la versión corta es que las redes neuronales de muchas capas se vuelven muy difíciles de entrenar dado el problema de desaparición de gradiente. En su lugar, la mayoría de las redes neuronales actuales usan otro tipo de función de activación llamada rectified linear unit o ReLU. A pesar del nombre complicado, se define simplemente como \(R(z) = max(0, z)\).
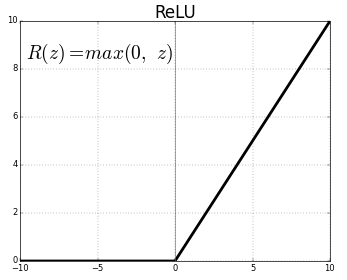
En otras palabras, las ReLUs permiten el paso de todos los valores positivos sin cambiarlos, pero asigna todos los valores negativos a 0. Aunque existen funciones de activación aún más recientes, la mayoría de las redes neuronales de hoy utilizan ReLU o una de sus variantes.
Independiente de la función de activación que utilicemos, podemos visualizar una neurona individual con el siguiente diagrama, una visualización representativa e intuitiva del comportamiento de una neurona.

Este diagrama muestra una neurona con tres entradas, que genera un único valor \(y\) como salida. Como en el caso anterior, primero calculamos la suma ponderada de sus entradas, y después pasamos la suma a través de una función de activacion sigmoide \(\sigma\).
\[z = b + w_1 x_1 + w_2 x_2 + w_3 x_3 \\ y = \sigma(z)\]Quizás te estás preguntando cuál es el propósito de una función de activación, y por qué preferimos usarla en lugar de de la suma ponderada – como lo hacemos con el clasificador lineal del capítulo anterior. La razón es que la suma ponderada, \(z\), es lineal con respecto a sus entradas. En cambio, las funciones de activación no-lineales nos ayudan a modelar funciones curvas o no triviales. Esto quedará más claro en la siguiente sección.
Capas
Ahora que hemos descrito una neurona, podemos definir una red neuronal. Una red neuronal consiste en una serie de capas de neuronas. Específicamente, todas las neuronas de una capa se conectan a las neuronas de la siguiente capa.
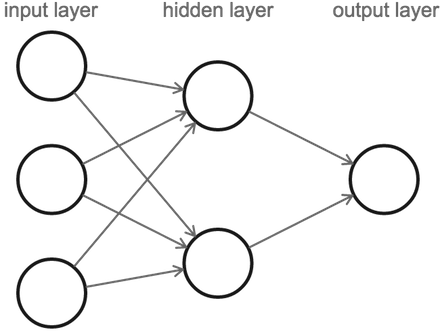
Un detalle es que cuando contamos el número de capas en una red neuronal, sólo contamos las capas con entradas (omitimos la primera capa de entrada). La figura anterior representa una red neuronal de 2 capas con 1 capa oculta. Contiene 3 neuronas de entrada, 2 neuronas en la capa oculta, y 1 neurona de salida.
Nuestro cálculo comienza con la capa de entrada a la izquierda, de la cual pasamos valores a la capa oculta. De ahí, la capa oculta envía valores de salida a la última capa, que contiene el valor final.
Aunque pareciera que cada una de las tres neuronas de entrada envía múltiples valores de salida a la capa oculta, en realidad solamente hay un valor de salida por neurona. Las neuronas siempre producen un valor, independientemente de cuántas conexiones de salida tengan.
Regresión
Llamamos propagación hacia delante (en inglés, forward propagation o forward pass) al proceso por el cual una red neuronal envía su entrada a través de sus capas hacia la salida. A las redes neuronales que funcionan de esta manera se les llama red neuronal prealimentada (en inglés, feedforward neural network). Ya pronto veremos que algunas redes neuronales permiten que los datos fluyan en círculos.
Por ahora demostraremos una propagación hacia delante con este ejemplo interactivo. Dale click al botón ‘Siguiente’ en la esquina superior derecha para continuar.
Más capas, más capacidad de expresión
¿Por qué son tan útiles las capas ocultas? La razón es que si no tuvieramos capas ocultas y tuvieramos que trazar una conexión directa entre nuestras entradas y nuestra salida, la contribución de cada entrada hacia el valor de salida sería independiente de las otras entradas. En la mayoría de los problemas del mundo real, las variables de entrada tienden a ser altamente interdependientes y afectan la salida de forma combinatoria y compleja. Las neuronas de las capas ocultas nos permiten capturar interacciones sutiles entre nuestras entradas.
Otra manera de interpretar esta idea es que las capas ocultas representan “características” a nivel superior o atributos de nuestros datos. Cada una de las neuronas de una capa oculta sopesa sus entradas de forma diferente, y de esta manera aprende características diferentes de los datos. Nuestra neurona de salida logra capturar estas características intermediarias, no sólo las entradas originales. Al incluir más de una capa oculta, permitimos que la red neuronal pueda aprender sobre varios niveles de abstracción de los datos. En el próximo capítulo aprenderemos más sobre las capas ocultas y sobre esta noción de características de alto nivel.
Recuerda también que las funciones de activación permiten capturar relaciones no lineales entre entradas y salidas. Si encadenamos múltiples transformaciones no lineales a través de las capas, aumentamos la flexibilidad y capacidad de expresión de la red neuronal. Aunque la prueba es compleja y mucho más avanzada de lo que podemos cubrir en este libro, se puede demostrar que cualquier red neuronal de 2 capas con una función de activación no lineal (incluyendo la sigmoide o ReLU) y con suficientes neuronas ocultas es un aproximador de función universal (en inglés, universal function approximator), es decir teóricamente es capaz de expresar cualquier mapeo arbitrario de entrada-a-salida. Las redes neuronales son poderosas precisamente por esta propiedad.
Clasificación
¿Qué sucede con la clasificación? En el capítulo anterior, introducimos la clasificación binaria al fijar un umbral para la salida en 0. Si nuestra salida era positiva, la clasificábamos como positiva; si nuestra salida era negativa, la clasificábamos como negativa. Podríamos adaptar este método para la neurona final de una red neuronal y clasificar la salida de acuerdo a algún umbral. Por ejemplo, podríamos establecer un umbral de 0.5 para clasificar las neuronas sigmoides que fueran positivas.
¿Qué sucede si tenemos varias categorías? Podríamos hacer que diferentes intervalos de valores en la neurona de salida correspondieran a diferentes categorías, aunque este método resultaría problemático por razones que cubriremos en el capítulo de la formación de redes neuronales. En vez de esto, la mejor manera de adaptar una red neuronal para la clasificación es dejar que cada neurona de salida corresponda a una categoría singular. Al realizar una propagación hacia delante, nuestra predicción llegaría a ser la neurona con el valor más alto. Veamos un ejemplo.
Clasificación de dígitos escritos a mano
Exploremos un problema real de clasificación: cómo reconocer y etiquetar dígitos escritos a mano. Usaremos un conjunto de datos llamado MNIST, que contiene 60,000 imágenes de dígitos, cada una etiquetada y midiendo 28x28 píxeles. La exactitud de clasificación de MNIST se usa como un punto de referencia común en el mundo del aprendizaje de máquinas. A continuación presentamos una muestra aleatoria de imágenes de este conjunto de datos:

Para clasificar estas imágenes podemos configurar una red neuronal de tal modo que las entradas de nuestra primera capa sean los valores de cada píxel. La red también debe contar con 10 neuronas de salida, una para cada categoría de dígito de 0 a 9. Como estamos trabajando con imágenes a escala de grises, cada píxel tiene un valor de luminosidad entre 0 (negro) y 255 (blanco). Todas las imágenes de MNIST son de 28x28, asi que contienen 784 píxeles en total. Podemos organizar todos estos píxeles en una sola matriz de entradas, como en el siguiente diagrama:

Aunque esta red parece mucho más complicada que nuestra simpre red 3x2x1 del capítulo anterior, funciona de la misma manera, con muchas más neuronas. Cada una de las neuronas de la primera capa oculta recibe todas de las entradas de la primera capa. En la capa de salida ahora tenemos diez neuronas en lugar de una, pero igual que en el ejemplo anterior, conectamos todas esas neuronas con la capa oculta anterior. Asignamos una etiqueta a cada una de las neuronas de salida; la primera corresponde al dígito 0, la segunda al dígito 1, y así sucesivamente.
Después de entrenar nuestra red – algo que cubriremos en detalle en otro capítulo – podemos predecir el dígito de cualquier muestra desconocida al pasar la muestra por la misma red y observar el valor de salida. La neurona de salida con el valor más alto corresponde al dígito predicho. El siguiente ejemplo demuestra el proceso; dale clic al botón “siguiente” para ver más predicciones.