En el capítulo anterior, vimos cómo entrenar una red neuronal para clasificar dígitos escritos a mano con una precisión de alrededor de 90%. En este capítulos vamos a evaluar el rendimiento de la red con más cuidado y también a examinar su estado interno para desarollar una intuición sobre lo que en realidad está sucediendo. Más adelante en el capítulo, nos toparemos con los límites de esta red neuronal al intentar entrenarla con un conjunto de datos de objetos como perros, automóbiles y barcos. De esta manera anticiparemos qué tipo de innovaciones serán necesarias para mejorar nuestra red y llevarla al siguiente nivel.
Visualizar pesos
Consideremos una red entrenada para clasificar dígitos MNIST escritos a mano. A diferencia del capítulo anterior, haremos un mapeo directo desde la capa de entrada hasta la capa de salida, de tal manera que nuestra red neuronal no tendrá capas ocultas. La red se verá de la siguiente manera:
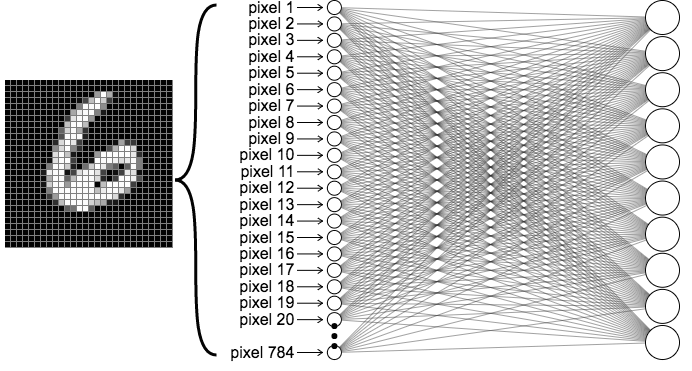
Recuerda que cuando pasamos una imagen a través de la red neuronal, podemos visualizar el diagrama de la red al “desenrollar” los píxeles de la imagen en una sola columna de neuronas, demostrado en la figura de la izquierda. Concentrémonos en las conexiones de la primera neurona de salida, que llamaremos \(z\). Etiquetaremos cada una de las neuronas de entrada y sus pesos correspondientes como \(x_i\) y \(w_i\).

Ahora veamos los pesos en una cuadrícula de 28x28, donde la posición de cada peso coincide con su píxel correspondiente. La representación anterior a la derecha se ve diferente a la siguiente figura, aunque ambas expresan la misma ecuación \(z=b+\sum{w x}\).
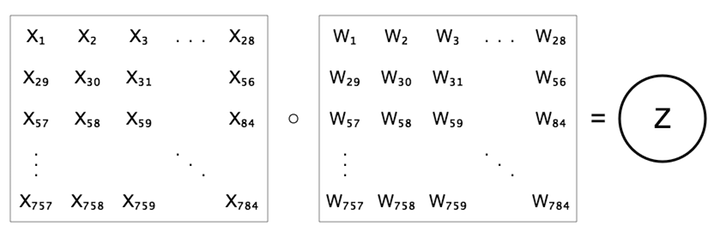
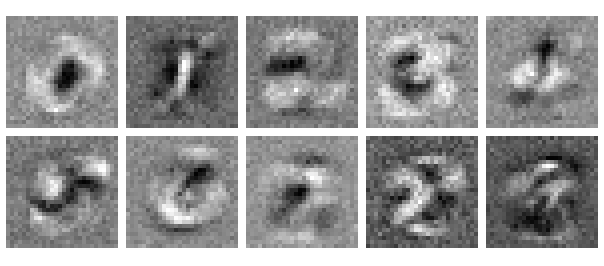
Ahora imaginemos una red neuronal entrenada con esta arquitectura y visualicemos los pesos aprendidos que sirven de entrada a la primera neurona de salida, la cual es responsable de clasificar el dígito 0. Representaremos los pesos más bajos con negro y los más altos con blanco.

Mira con cuidado… ¿Se parece un poco a un 0 borroso? La razón por la que parece así quedará clara si pensamos en lo que esta neurona está haciendo. Debido a que es “responsable” de clasificar 0s, su objetivo es generar un valor alto para los 0s y un valor bajo para los dígitos que no sean 0. La neurona podrá obtener salidas altas para los 0s si asocia pesos altos con píxeles que tienden a ser altos en imágenes de 0s. De la misma manera, puede obtener salidas relativamente bajas para dígitos que no son 0 al asociar pesos bajos con píxeles que tienden a ser altos en imágenes de dígitos que no son 0. Por ejemplo, el centro relativamente negro de la imágen de los pesos se da porque la mayoría de las imágenes de 0s no corresponden con esta área (dado el agujero del 0).
Veamos los pesos que la red neuronal aprendió para cada una de las neuronas de salida. Como sospechamos, cada una se ve como una versión borrosa de los diez dígitos. Parece que hubiésemos tomado el promedio de muchas imágenes de cada dígito.
Supongamos que usemos una imagen de un 2 como entrada. Podemos anticipar que la neurona responsable de clasificar los 2 tendrá un valor alto porque sus pesos son tales que corresponden con los píxeles que tienden a representar un 2. En el caso de otras neuronas, algunos de los pesos también corresponderán a píxeles altos. Sin embargo, coincidirán mucho menos y esos valores altos serán negados por pesos bajos en la neurona del 2. La función de activación no cambia eso, porque es monótona con respecto a la entrada, es decir, cuanto mayor la entrada, mayor será la salida.
Podemos interpretar que los pesos están formando modelos de las clases de salida. Esto es realmente fascinante porque nunca le dijimos a nuestra red de antemano lo que era un dígito y sin embargo logró parecerse a esa clase de objetos. Esto sugiere lo verdaderamente especial en las redes neuronales: forman representaciones de los objetos con los cuales son entrenadas - y resulta que estas representaciones no sólo son útiles para la clasificación y predicción. Hablaremos más sobre esta capacidad de representación cuando lleguemos a las redes neuronales convolucionales más adelante…
Quizás esta discusión te ha generado más preguntas que respuestas. Por ejemplo, ¿qué ocurre con los pesos cuando añadimos capas ocultas? La respuesta a esto se basará en algo que vimos en la sección anterior. Pero antes de llegar a eso, será beneficioso examinar el rendimiento de nuestra red neuronal, y en particular considerar qué tipo de errores tiende a cometer.
0op5, l0 h1ce 0tra v3z
De vez en cuando nuestra red neuronal cometerá errores con los que podremos simpatizar. A mi parecer, no es tan obvio que el primer dígito en la siguiente imagen sea un 9. Se parece a un 4, que fue lo que nuestra red pensó que era. De la misma manera, podemos entender por qué el segundo dígito, un 3, fue clasificado erróneamente como un 8. Por otro lado, los errores del tercer y cuarto dígito son más serios. Cualquier persona podría reconocerlos como un 3 y un 2, respectivamente. Sin embargo, nuestra red neuronal pensó que el tercer dígito era un 5 y no tiene mucha idea sobre el cuarto dígito.

Investiguemos el rendimiento de la red neuronal del capítulo anterior, que logró alcanzar una precisión de 90% con los dígitos MNIST. Una manera de hacer esto es con una matriz de confusión: una manera de listar nuestras predicciones en una tabla. En la siguiente matriz de confusión, las 10 filas corresponden a las etiquetas reales del conjunto de datos MNIST y las columnas representan las etiquetas predichas. Por ejemplo, la celda en la cuarta fila y la sexta columna nos dice que hubo 71 casos donde un 3 real fue etiquetado por la red neuronal como un 5. La diagonal verde en esta matriz nos muestra la cantidad de predicciones correctas. Todas las otras celdas muestran errores.
Coloca el cursor del ratón sobre cada celda para obtener una muestra de las instancias que representa esa celda, ordenadas en base a la confianza (probabilidad) de cada predicción.
También podemos aprender algo importante al trazar la muestra más alta de cada celda de la matriz de confusión, como puedes ver a continuación:
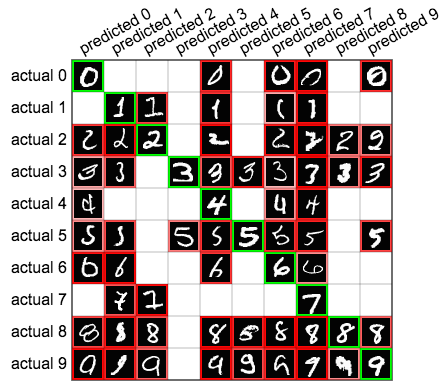
Esto nos da una impresión de cómo la red aprende a hacer ciertas predicciones. En las primeras dos columnas podemos ver que la red parece estar buscando los círculos que predicen un 0 y las líneas delgadas que predicen un 1. La red se confunde cuando otros dígitos presentan esas mismas características.
Cómo romper nuestra red neuronal
Hasta ahora sólo hemos visto redes neuronales entrenadas para identificar dígitos. Aunque hay mucho que aprender con este ejemplo, en realidad es un caso bastante simple: sólo tenemos 10 clases, bien definidas y con relativamente poca variación interna entre ellas. En la mayoría de los casos del mundo real, estamos tratando de clasificar imágenes en circunstancias menos ideales. Veamos el rendimiento de esta misma red neuronal aplicado a CIFAR-10, otro conjunto de datos etiquetados de 60.000 imágenes a color (de 32x32 píxeles) de aviones, automóviles, pájaros, gatos, venados, perros, ranas, caballos, barcos y camiones. Aquí está una muestra aleatoria de imágenes de CIFAR-10.

De inmediato, nos queda claro que estas clases de imágenes son muy diferentes a las que llevamos investigando. Por ejemplo, los gatos pueden aparecer orientados en diferentes direcciones, presentar colores y pelaje diferente, estar estirados o encogidos, y muchas otras variaciones que los dígitos escritos a mano no presentaron.
Efectivamente, si entrenamos una red neuronal de dos capas con estas imágenes, lograremos una precisión de apenas 37%. Sigue siendo mejor que una conjetura al azar (la cual nos daría una precisión de 10%), pero está muy por debajo del 90% que alcanzamos con el clasificador MNIST. Ya veremos que las redes neuronales convolucionales mejorarán ambos casos enormemente. Por ahora, podremos explorar las deficiencias de las redes neuronales normales al explorar sus ponderaciones.
Repitamos el experimento anterior de observar los pesos de una red neuronal de sólo 1 capa sin capas ocultas, excepto que esta vez utilizaremos las imágenes de CIFAR-10. Los pesos aparecen a continuación.

Comparados a los pesos de MNIST, estos tienen menos rasgos discernibles. Algunos detalles sí tienen sentido: los aviones y los barcos presentan tonos azules en el borde exterior, lo cual refleja que estas imágenes tienden a tener cielos azules o agua a su alrededor. Ya que la imagen de ponderaciones para cualquiera de estas clases está relacionada con un promedio de las imágenes pertenecientes a esa clase, podemos esperar que salgan colores promedios. Sin embargo, ya que las clases de CIFAR-10 son mucho menos consistentes internamente, es más díficil reconocer patrones discernibles.
Veamos la matriz de confusión asociada con este clasificador CIFAR-10:
Su rendimiento es muy pobre - alcanza apenas un 37% de precisión. Claramente nuestra pequeña red de 1 capa no es capaz de capturar la complejidad de nuestro conjunto de datos. Pero podemos mejorar su rendimiento introduciendo una capa oculta. En la próxima sección analizaremos los efectos de esta capa.
Capas ocultas
Hasta ahora nos hemos enfocado en redes neurales de una capa, donde las entradas se conectan directamente a las salidas. ¿Cuál es el efecto de las capas ocultas en las redes neuronales? Intentemos insertar una capa intermedia de 10 neuronas a nuestra red de MNIST. Nuestra red se vería de la siguiente manera.

En cierto sentido, se podría decir que “forzamos” a nuestra red original de 1 capa a aprender modelos para cada clase porque cada uno de los pesos se conectó directamente a una sola clase. En este caso ya no tenemos los 784 píxeles de entrada conectándose directamente a las clases de salida. Esta red es más complicada, ya que los pesos en la capa oculta afectan todas las diez neuronas de la capa de salida. ¿Cómo se ven esos pesos ahora?
Para entender lo que está sucediendo primero vamos a visualizar los pesos en la primera capa, como lo hicimos antes. También veremos con cuidado cómo se combinan sus activaciones en la segunda capa para obtener los resultados de cada clase. Recuerde que una imagen generará una activación alta en una neurona de la primera capa si la imagen favorece ese filtro. Asi que las diez neuronas en la capa oculta reflejan la presencia de esas diez características en la imagen orginal. Cada neurona en la capa de salida (cada una corresponde a una etiqueta de clase) es una combinación ponderada de las diez activaciones previas. Veámoslo a continuación.
Empecemos con los pesos de la primera capa. Ya no se parecen a las clases de imágenes que vimos anteriormente, son más extrañas. Algunos parecen pseudodígitos y otros parecen ser components de dígitos: medios círculos, líneas diagonales, agujeros, etc.
Las filas debajo de las imágenes de filtro corresponden a nuestras neuronas de salida, una para cada clase. Las barras representan los pesos asociados a cada uno de los diez filtros de activación de la capa oculta. Por ejemplo, la clase 0 parece favorecer los filtros de la primera capa, que tienen valores altos en el borde exterior (donde tiende a aparecer el dígito cero). En cambio, desfavorece filtros donde hay valores bajos en los píxeles del medio (donde aparece el agujero del cero). La clase 1 es casi lo opuesto: prefiere filtros que presentan valores altos en el medio, donde podríamos esperar el trazo vertical de un 1.
La ventaja de esta estrategia es la flexibilidad. Para cada clase, hay una gama mucho más amplia de patrones que estimulan la neurona de salida correspondiente. Cada clase puede ser activada por la presencia de varias características abstractas de la capa oculta anterior. De esta manera podremos aprender a distinguir varios tipos de ceros, varios tipos de unos, etc. para cada clase. Casi siempre (aunque no en todos los casos) esto mejorará el rendimiento de la red neuronal.
Características y representaciones
Generalicemos algo de lo que hemos aprendido en este capítulo. En las redes neuronales de una o más capas, cada capa tiene una función similar: transformar la data de la capa anterior en una representación de “alto nivel” - es decir, una representación más compacta y saliente de los datos (de la misma manera que un resumen es una representación compacta de un libro). Por ejemplo, en la primera capa de la red anterior hicimos un mapeo de píxeles de “bajo nivel” a características de “alto nivel” que representan las diferencias entre dígitos (el tipo de trazo, qué tan circular es la forma, los agujeros que presenta, etc.). Esas características de “alto nivel” fueron a su vez mapeadas a una representación aún más alta en la capa final: la de los dígitos actuales. Este proceso de transformar la data en información cada vez más concreta y expresiva es una noción muy importante en el aprendizaje de máquinas, y es la ventaja principal de las redes neuronales.
Cuando agregamos capas ocultas a una red, le damos la oportunidad de aprender características a varios niveles de abstracción. Las capas iniciales aprenden a representar característias de “bajo nivel” y las capas finales características más expresivas, pero que en realidad están compuestas de las características de las capas anteriores.
Las capas ocultas pueden mejorar el rendimiento de una red, pero sólo de forma limitada. Aunque agreguemos más y más capas ocultas a una red, en algún momento su rendimiento dejará de mejorar -no podemos simplemente pedirle a nuestra red que memorice todas las versiones posibles de una clase a través de sus capas ocultas-. Existe una mejor manera utilizando redes neuronales convolucionales, un tema que presentaremos en otro capítulo.
Recursos adicionales
Próximo capítulo
En el próximo capítulo aprenderemos sobre un tema crítico que sólo hemos mencionado superficialmente: cómo se entrenan las redes neuronales, el proceso por el cual se construyen y entrenan estas redes usando una técnica llamada descenso de gradiente via retropropagación. Aprenderemos primero sobre la regresión lineal simple y, a través de ejemplos, presentaremos varios aspectos importantes a considerar al entrenar una red neuronal.