translated by Kynd and Naoto Hieda
自分を山の頂上にいる登山家だと想像してください。夜が訪れてしまいました。麓にあるベースキャンプに戻る必要がありますが、暗い中で貧弱な懐中電灯しか持っておらず、目の前にある1メートル程度先の地面しか見ることができません。この際にどのように下りるのが一番良いのでしょう。戦略の1つは、あらゆる方向を見てどの道が最も急に下っているのかを見極め、その方向に進むことです。このプロセスを何回も繰り返すと、徐々に山を下りることができるでしょう。たまに小さな凹みや谷に嵌るかもしれません。その場合は、勢いをつけてもう少し進むことで抜け出すことができます。細かな欠点は置いておくとして、この戦略に従えば最終的には麓まで辿り着くことができます。
このシナリオはニューラルネットワークとは関係ないように見えるかもしれませんが、実はどのようにネットワークを訓練するのかの良い例え話になっています。実際、その主な手法である勾配降下法は上で述べた話とよく似ています。訓練とは、ニューラルネットワークの精度を最大にするために使用する重みの集合を最適化することでした。前章では訓練のプロセスはブラックボックスにしてごまかしておき、訓練済みのネットワークに何ができるかを観察しました。本章の大部分は勾配降下法がどのように機能するかの詳細について割かれており、この手法が登山家の比喩に似ていることを見ていくことになります。
どのように訓練が行われるのかを正確に知らなくてもニューラルネットワークを使うことができるというのは、内部の電子回路がどのように機能するかを知らなくても懐中電灯を使えることに似ています。最新の機械学習ライブラリのほとんどは訓練を大幅に自動化しており、また、このトピックで扱う数学は難しいので、訓練については脇に置いてニューラルネットワークの実際の活用法に向かって先を急いでしまいたくなるかもしれません。しかし勇敢な読者の皆さんにはこれが間違いだとわかっているはずです。プロセスを理解することで初めて、ニューラルネットワークをどのように用いたり構築し直したりするか、貴重な理解を得ることができるからです。それだけでなく、長年の間達成できなかった大規模なニューラルネットワークの訓練が最近になってやっと実現可能になったこということは、人工知能の歴史における大きな成功例の1つであり、その手法は今、最も活発で興味深い研究分野の1つなのです。
本章の目的は、ニューラルネットワークがどのように最適化されるかについて厳密とは言わないまでも、直感的に理解することです。数式よりもできるだけ視覚的な情報を優先し、更に読み知識を深めるための外部リンクも途中で紹介していきます。勾配降下法、バックプロパゲーション、および関連するすべての手法について順次説明していきますが、その前にまず、なぜ訓練が難しいのかを理解しましょう。
なぜ訓練は難しいのか
超次元の干し草の中から針を探す
隠れ層を持つニューラルネットワークの重みは相互に強く依存しています。なぜか調べるために、次の3層ネットワークの第1層の、赤く強調された接続について考えます。この接続の重みを少しでも調整すると、直接伝播するニューロンだけでなく以降の2層のすべてのニューロンにも影響を与え、結果として全ての最終出力に反映されます。
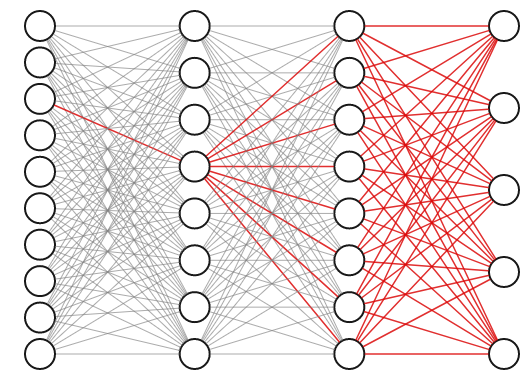
そのため、重みを1つずつ順番に最適化していくことでは最適な重みの組み合わせを得ることはできません。可能な重みの組み合わせ全てが含まれる空間全体を同時に探索しなければならないのです。これはどのようにして行うのでしょうか。
重みの組み合わせを選ぶ最も単純で素朴な手法から始めましょう。ネットワークの全ての重みをランダムな値に設定し、データセットに対して正解率を評価します。これを何度も繰り返し結果を記録していき、最も正確な結果を出力した重みの組み合わせを残します。一見これは合理的な手法のように思えるかもしれません。何といってもコンピュータは高速なので、ブルートフォースでもまともな解を得ることができるでしょう。 数十のニューロンしかないネットワークならばこれでうまく行きます。数多の推測を素早く試みることができ、そこからまともな候補を得られるはずです。 しかし、実際のほとんどの応用例には、それよりもはるかに多くの重みがあります。前章の手書き数字の例を考えてみましょう。そこには約12,000の重みがあります。その中で最高の組み合わせを見つけるのは、干し草の中から針を探すようなものですが、この干し草は12,000もの次元を持っています!
訳注:needle in a haystack は直訳すると干し草の中から針を探す、転じて望みのない捜し物をすることです(Weblio英和辞典)。
読者の皆さんは、12,000次元の干し草はよりなじみのある3次元の干し草よりも「4,000倍大きいだけ」なので、最適な重さを発見するためには4000倍の時間がかかるだけと考えているかもしれません。しかし、次の節で説明するように、現実にはその比率はそれよりも途方もなくはるかに大きいのです。
n-次元空間は孤独な場所
ブルートフォースに検索した場合、納得のいく重みの組み合わせを得るまでにはどれくらいの試行が必要でしょうか。直観的に考えると、十分な数の試行を行い、可能な試行全体の空間を高密度にサンプリングをする必要がありそうです。事前知識がないとどこに最適な重みの組み合わせが隠れているかわからないので、可能な限りサンプリングするのは理にかなっています。
これを説明するために、入力層に2つのニューロンを持った非常に小さな1層ニューラルネットワークと、同じく3つのニューロンを持ったネットワークを考えてみましょう。便宜上バイアスは省きます。

最初のネットワークには重みが2つあります。確信を持って適当な解にたどりつけるようにするには何度の試行が必要でしょうか。この問題に取り組む方法の1つは、可能な重みの全ての組み合わせを含む2次元空間を、ある一定の精度でもれなく検索することです。それぞれの軸に沿って10分割することを考えます。その場合、試行数は2つの軸上の区間全ての組み合わせで、合計100になります。これはそれほど悪くありません。このくらいの精度でサンプリングすれば空間のほとんどをかなり良くカバーできます。軸を10分割ではなく100分割にすると、100 * 100 = 10,000回となり、空間をとても密にカバーできます。10,000回ならまだかなり少ないもので、どのコンピュータも1秒未満で網羅できるでしょう。
2つ目のネットワークの例ではどうでしょう。2つではなく3つの重みがあるため3次元空間から答えを探します。この空間を先の例と同じ精度でサンプリングするとして、同様に各軸を10分割します。今回は \(10 * 10 * 10 = 1,000\) 回の試行になります。2次元と3次元両方のケースを下の図に示します。
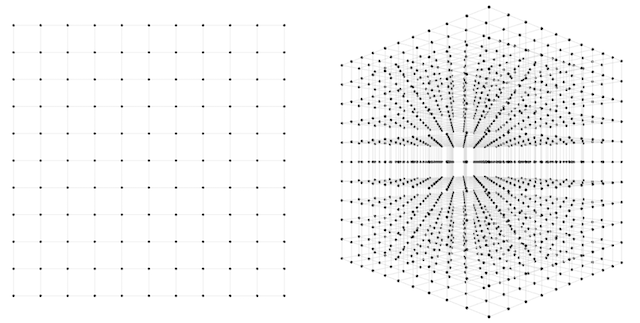
1,000回の試行なら楽なものだと言えるかもしれません。100分割した精度の場合、\(100 * 100 * 100 = 1000000\) 回の試行になります。1,000,000回ならまだ問題にはなりませんが、だんだんと不安になってきたでしょう。この手法をより現実的な規模のニューラルネットワークに拡大するとどうなるでしょうか。可能な試行数は、推測する重みの数に対して指数関数的に増加することがわかります。1軸につき10分割の精度でサンプリングする場合、\(N\) 次元のデータセットには一般に \(10^N\) のサンプルが必要です。
それでは、この手法を用いてニューラルネットワークで見たMNISTデータセットを分類するネットワークを訓練するとどうなるでしょうか。ネットワークには784個の入力ニューロン、隠れ層に15個のニューロン、出力層に10個のニューロンがあることを思い出してください。つまり、\(784*15 + 15*10 = 11910\) 個の重みがあります。 25個のバイアスを加えると、11,935次元の変数を同時に推測する必要があります。つまり、私たちは \(10^{11935}\) 回の試行をしなければならないということです…それは、1の後におよそ12,000個の0が続く数です!これは想像を絶するほどの大きな数字です。比較の為に言うと、宇宙全体には \(10^{80}\) 個の原子しか存在しません。どんなスーパーコンピューターでもこれほど多くの計算をすることは考えられないでしょう。実際、今日世界に存在するすべてのコンピュータを用いて地球が太陽に衝突するまでの間計算しても、まだ計算が終わるには程遠いのです!さらに、近年のディープニューラルネットワークにはしばしば数千万から数億個の重みがあることも考慮してください。
この法則は、機械学習で「次元の呪い」と呼ばれるものと密接に関連しています。探索する空間に次元を追加するごとに、訓練するモデルを最適化するのに必要なサンプルの数は指数関数的に増加します。次元の呪いはしばしばデータセットのことを指します。端的には、データセットを構成する列や変数が多いほど、モデルを得るために必要なデータセットのサンプルの数は指数関数的に増加します。この例では入力データの次元ではなく重みの数を考えていますが、原則は同じです。 高次元空間は巨大なのです!
明らかに、重みの最適化にはランダムに推測するよりも洗練された解決策が必要です。最適化の問題を解決するための効率的な計算手法について理解を深めるために、少しの間ニューラルネットワークのことを忘れて、よりシンプルな問題を解くことから始めます。そして勾配降下法にたどり着くまで徐々にスケールアップしていきましょう。
線形回帰
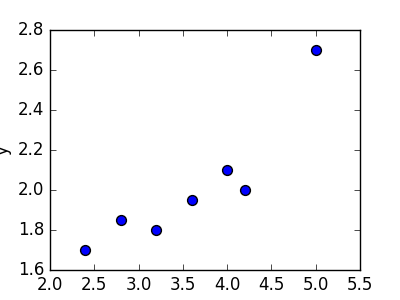
線形回帰とは、あるデータの集合に対して「最もうまく当てはまる直線」を求めるための手法です。ニューラルネットワークを解くために使う非線形な手法よりも簡単で、以前から使われていました。 例を見ましょう。 左下の表に示した7つの点の集合が与えられたとします。 表の右側には、これらの点の散布図があります。
| 2.4 | 1.7 |
| 2.8 | 1.85 |
| 3.2 | 1.79 |
| 3.6 | 1.95 |
| 4.0 | 2.1 |
| 4.2 | 2.0 |
| 5.0 | 2.7 |
線形回帰の目的は、これらの点に最もよく合う直線を見つけることです。 直線の一般的な方程式は、線の傾きを \(m\)、y切片を \(b\) とすると、\(f(x) = m \cdot x + b\) となることを思い出してください。 したがって線形回帰を解くとは、\(f(x)\) ができるだけ \(y\) に近づくよう、\(m\) および \(b\) の最も良い値を決定するということになります。 いくつかランダムな候補を試してみましょう。
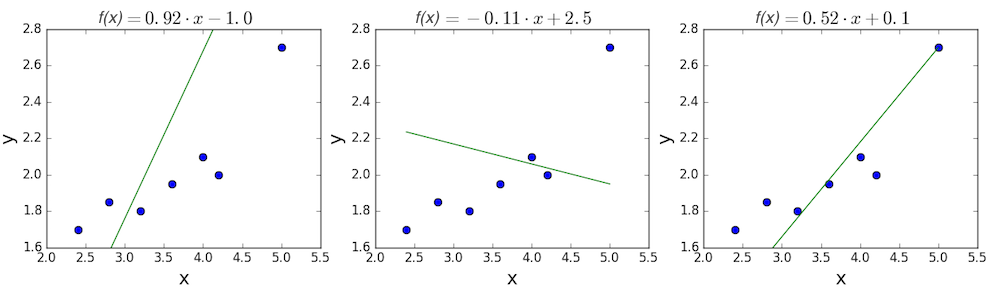
最初の2つの直線はどう見てもデータとうまく合っていません。3番目は他の2つよりも少しましに見えます。定量的に決めるにはどうすれば良いのでしょう。線の適合具合を表す方法が必要です。損失関数を定義することでこれを実現できます。
損失関数
損失関数(別名:コスト関数)は線形回帰の直線とデータとの誤差の量を測るために用いられます。損失関数には様々な種類がありますが、どれも基本的にはある \(x\) の値と、データセットの実際の値との距離に応じてペナルティを計算します。中央の図、\(f(x) = -0.11 \cdot x + 2.5\) を例にとると、実際の値と予測値との差は赤い点線で示したようになります。
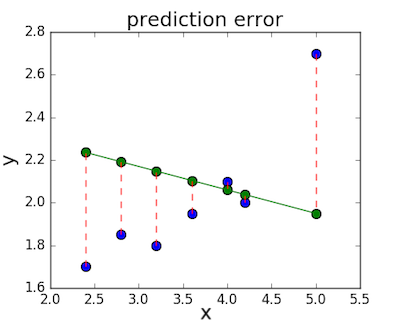
とても一般的な関数の1つに平均二乗誤差 (MSE)があります。MSEを計算するには単純に全ての誤差(点線)の長さをそれぞれ二乗し、その平均を求めます。
\[MSE = \frac{1}{n} \sum_i{(y_i - f(x_i))^2}\] \[MSE = \frac{1}{n} \sum_i{(y_i - (mx_i + b))^2}\]上で示した3つの直線の一次関数についてMSEを計算して見ましょう。最初の直線は0.17、2番目は0.08となり、3番目は0.02と小さい値になります。思った通り3番目の直線のMSEが最小となり、これが最も良く適合しているという予測が正しいことが確かめられました。
ある狭い範囲に含まれる \(m\) と \(b\) 全てに対してMSEを計算して比較すると、より直感的な理解を得られます。下の図について考えてみてください。傾き \(m\) が-2から4の間、切片 \(b\) が-6から8の間の平均二乗誤差を2つの異なる方法で可視化したものです。
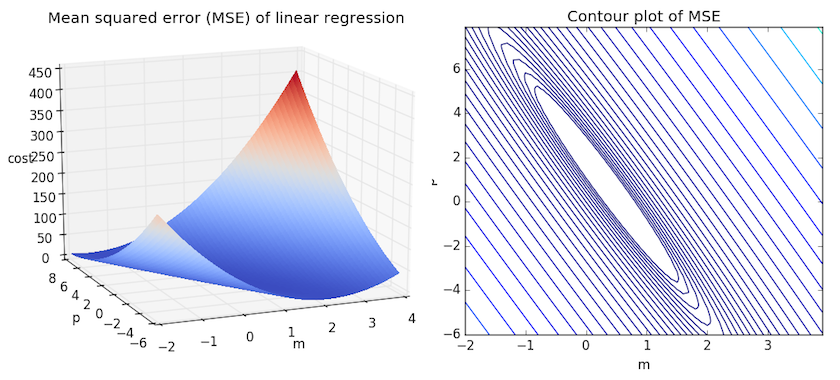
右:同じ図を、対数的に等間隔な2次元の等高線図として可視化したもの
上の2つのグラフを見ると、このMSEは引き伸ばしたお椀のような形をしていて、およそ \((m,p) \approx (0.5, 1.0)\) を中心とする楕円の範囲で平らになっていることがわかります。実際に任意のデータセットの線形回帰のMSEをプロットすると、これに似た形になります。MSEを最小にしたいので、このお椀の中の最も低い点を見つけることが目標となります。
次元をさらに増やす
上記は最小限の例で、1つの独立変数 \(x\) と2つのパラメータ \(m\) と \(b\) しかありません。より多くの変数がある場合はどうなるでしょうか。一般に、\(n\) 個の変数をもつ一次関数は次のように書くことができます。
\[f(x) = b + w_1 \cdot x_1 + w_2 \cdot x_2 + ... + w_n \cdot x_n\]または、行列を用いて次のようにまとめることができます。
\[f(x) = b + W^\top X \;\;\;\;\;\;\;\;where\;\;\;\;\;\;\;\; W = \begin{bmatrix} w_1\\w_2\\\vdots\\w_n\\\end{bmatrix} \;\;\;\;and\;\;\;\; X = \begin{bmatrix} x_1\\x_2\\\vdots\\x_n\\\end{bmatrix}\]これを簡略化するにはバイアス $b$ を単純にもう1つの重みと考え、ダミーの入力値として常に1を掛ける方法があります。つまり下の式のようになります。
\[f(x) = W^\top X \;\;\;\;\;\;\;\;where\;\;\;\;\;\;\;\; W = \begin{bmatrix} b\\w_1\\w_2\\\vdots\\w_n\\\end{bmatrix} \;\;\;\;and\;\;\;\; X = \begin{bmatrix} 1\\x_1\\x_2\\\vdots\\x_n\\\end{bmatrix}\]この行列の形は前の式と等価でありながら、表記法としても、概念的にも便利です。$f(x) = W^\top X$ と単純な形で書くことができ、バイアスを単に、もう1つの最適化が必要な重みと考ることができるからです。
次元の数を増やすと問題がひどく複雑になるように思うかもしれませんが、2次元、3次元、または任意の次元数でも式の形は全く同じままです。もう図に描くことはできませんが、多次元の中にもお椀(ボウル)のように見える損失関数、ハイパーボウルが存在するのです。これまでと同じく目標はお椀の最下部を探すこと、つまり客観的には選択したパラメータとデータセットに応じた損失関数の最小値を探すことです。
現実には、その最下部の点の場所をどのように計算するのでしょうか。いくつかの方法がありますが、最も一般的な方法はこの問題を解析的に解く最小二乗法です。解くべき変数が1つまたは2つしかない場合は手作業でも行うことができ、一般に統計や線形代数の入門講義で教えられています。
非線形性の呪い
残念なことに一般的な最小二乗法ではニューラルネットワークは最適化できませんので、上記の線形回帰の問題は読者の皆さんの課題とします。線形回帰を使用できない理由はニューラルネットワークが非線形であるためです。先の一次方程式とニューラルネットワークの主要な違いは、活性化関数(シグモイド、tanh(双曲線正接)、ReLU等)の有無にあることを思い出してください。したがって、上の線形方程式は単に \(y = b + W^\top X\) ですが、対してシグモイド活性化関数を用いる1層ニューラルネットワークの式は \(f(x) = \sigma (b + W^\top X)\) となります。
非線形性は、パラメータが相互に関係しながら損失関数の形状に影響を及ぼすことを意味します。ニューラルネットワークの損失関数は椀型に比べてより複雑で、山と谷でいっぱいです。「椀型」の特性は凸関数と呼ばれ、複数変数の最適化において貴重な利便性があります。凸な損失関数には必ず全区間での最小値(お椀の底)があり、下り坂の道全てがその最小値に続いています。
しかし、非線形性を導入し、ニューラルネットワークをより「柔軟」で任意の関数をモデル化できるようにしたことで、凸関数の利便性を失ってしまいました。1つのステップで解析的に最小値を見つける簡単な方法はもはや存在しません(つまり、整った等式を導くことはできないのです)。この場合は解にたどり着くために、複数のステップに渡る数値解析を使用せざるを得ません。いくつかの手法が存在しますが、勾配降下法が中でも最も一般的で効果的です。次節では、その仕組みについて説明します。
勾配降下法
これまで見てきたような、目的関数を満たすためのパラメータを見つけることは、機械学習に特有の問題ではありません。それは数理最適化の非常に一般的な問題として長い間知られており、ニューラルネットワーク以外の様々な場面でも見かけられます。今日、ニューラルネットワークの訓練を含む多変数関数の最適化問題の多くには、線形回帰よりもずっと強力で、ランダムに試行を繰り返すよりもずっと早く有力な解を求めることができる、勾配降下と呼ばれるアルゴリズムが用いられています。
勾配降下法のやり方
直感的に言えば勾配降下法の働きは、章の初めの登山家の話に似ています。まずランダムなパラメータから始めます。次に、どちらの方向に進むと(パラメータの変化に対して)損失関数の値が最も早く降下していくかを求め、その方向に少しだけ進みます。言い換えると損失関数の減少が最も大きくなるようなパラメータの調整の仕方を決めるのです。このプロセスを、最小の点が見つかったと納得できるまで繰り返します。
損失関数が最も早く降下していく方向を見つけるには、全てのパラメータに対して損失関数の勾配を計算する必要があります。勾配とは、微分を多次元に一般化したもので、関数に含まれるそれぞれの変数についての偏微分をベクトルにしたものです。損失関数のそれぞれの軸に沿った傾きを成分に持つベクトルと言い換えることもできます。
線形回帰を解くには、最小二乗法かその他の1ステップで終わる方法が最も向いていると述べました。しかし、あえて勾配降下法を使って線形回帰の解を求める簡単な例を見てみましょう。
前の節で見た平均二乗誤差のことを思い出してください。これを $J$ とします。
\[J = \frac{1}{n} \sum_i{(y_i - (mx_i + b))^2}\]最適化するパラメータは、 $m$ と $b$ の2つです。それぞれについて $J$ の偏微分を計算しましょう。
\[\frac{\partial J}{\partial m} = \frac{2}{n} \sum_i{x_i \cdot (y_i - (mx_i + b))}\] \[\frac{\partial J}{\partial b} = \frac{2}{n} \sum_i{(y_i - (mx_i + b))}\]勾配は求められましたが、どのくらいその方向に進むべきでしょうか。これは大事な判断で、一般的な勾配降下法ではこの値は手動で決められます。学習率と呼ばれるこの値は、最も重要かつ繊細なハイパーパラメータで、しばしば \(\alpha\) で表されます。\(\alpha\) が小さすぎると、谷底に到達するのに許容できないほどの長い時間がかかることがあります。\(\alpha\) が大きすぎると、正しい経路を進み過ぎてしまったり、坂を上に登ってしまったりすることがあります。
訳注:ここでのハイパーパラメータとは、それが最適化の対象となる関数に含まれるパラメータではなく、勾配降下法という最適化の「手段」を調整するためのパラメータだという意味です。
代入演算を $:=$ で表すと、2つのパラメータを更新するステップを以下のように書くことができます。
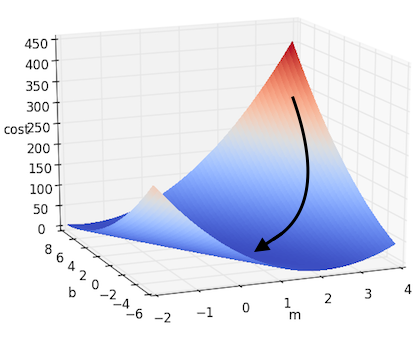
\[m := m - \alpha \cdot \frac{\partial J}{\partial m}\] \[b := b - \alpha \cdot \frac{\partial J}{\partial b}\]このアプローチで先に挙げたシンプルな線形回帰の例を解くと、下の図の様になります。
もっと多くの次元がある場合にはどうすれば良いのでしょう。それぞれのパラメータを $w_i$ とすると、$f(x) = b + W^\top X $ となり、上記の例を多次元の場合にも当てはめることができます。これは勾配を使って書くとより簡潔に表すことができます。$J$ の勾配を $\nabla J$ と書きます。勾配はそれぞれのパラメータに対する偏微分全てを含むベクトルであることを思い出してください。上記の更新ステップは下記のように表すことができます。
\[\nabla J(W) = \Biggl(\frac{\partial J}{\partial w_1}, \frac{\partial J}{\partial w_2}, \cdots, \frac{\partial J}{\partial w_N} \Biggr)\] \[W := W - \alpha \nabla J(W)\]この公式は一般的な勾配降下法の標準の形です。この式は線形回帰や全ての線形最適化問題に対して最良のパラメータの集合を導いてくれることが保証されています。この式の意味を理解すれば、ニューラルネットワークを訓練する方法の概要を理解したことになります。しかし実際のニューラルネットワークでは、いくつかの理由でこのプロセスはもっと複雑になります。次の節ではその対処法について説明します。
勾配降下法をニューラルネットワークに適用する
非凸関数の問題
前節では単純な線形回帰の問題に対して勾配降下法を実行する方法を示し、そうすることで必ず正しいパラメータを見つけることができると説明しました。これは線形のモデルには当てはまりますが、ニューラルネットワークには当てはまりません。活性化関数の影響でニューラルネットワークの損失関数は「お椀型」ではなく、凸関数でもありません。損失関数には多くの丘、谷、湾曲、その他の不規則な形があり、もっと複雑です。これは、多くの「極小値」、つまり損失関数が狭い範囲での最小値になるけれども、必ずしも絶対的な最小値(または「大域最小値」)にはならないパラメータの選び方が存在することを意味します。勾配降下法を実行する際に、誤って極小値に行き詰まってしまう可能性があるのです。
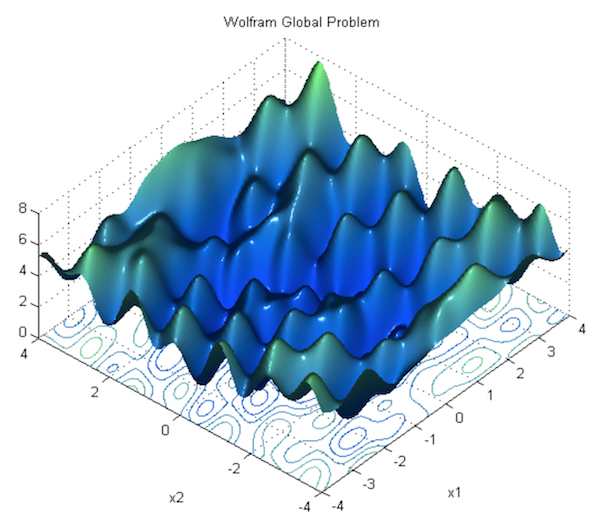
理論的な理由はこの本の範囲を超えますが、これはディープラーニングでは大きな問題にはなりません。隠れ層に十分な数のニューロンがあることとその他いくつかの条件を満たす場合、ほとんどの極小値はそれなりに全体の最小値に近く「十分に良い」からです。 Dauphinらによると局所最小値よりも、勾配が0に非常に近くなる鞍点の方がより大きな問題です。なぜそうなのかについてはYoshua Bengioによる講義 のsection 28, 1:09:41から始まる部分を見てください。
極小値は対した問題ではないとはいえ、全く問題にならないまで解決できればそのほうが良いでしょう。方法の1つとして、次の節で見るように勾配降下法のやり方を変えることができます。これについては次の節で扱います。
バッチ学習、確率的学習、ミニバッチ学習
極小値の他にも、「素の」勾配降下法にはもう1つ大きな問題があります。それは遅すぎることです。ニューラルネットワークには数億ものパラメータが存在することがあり、データセットから1つのサンプルを評価するためには何億回もの演算が必要になります。データセットの全てのデータに対して勾配降下法の評価を行う方法はバッチ勾配降下法とも呼ばれますが、非常にコストが高く低速です。また、どんなデータセットにも冗長性があり、十分な大きさの部分集合を取れば全てのデータを使った場合と近い結果が得られるので、勾配を求めるためにバッチ勾配降下法を用いるのは必要以上のコストを払っていることになります。
確率的勾配降下法(SGD: Stochastic Gradient Descent)と呼ばれる勾配降下法を修正したバージョンを用いると、計算コストと極小値、両方の問題に対処することができます。SDGではデータセットをシャッフルし、個別に取り出したサンプルごとに勾配を計算して、その都度重みを更新します。サンプルには異常値もあり、必ずしも実際の勾配に近い値が得られないこともあるので、一見これは良くないアイデアに思えるかもしれません。しかしランダムな順序でこれを行うと更新作業の全体のバラつきが平均化され、良い解に向かって収束するのです。またSGDは重みの更新の仕方をより「ギクシャクとした」不安定な動きにするため、極小値や鞍点から抜け出しやすくなります。
SGDは損失関数の曲面の形が不規則な場合に特に有用です。しかしより一般的には、ミニ・バッチ勾配降下法(MB-GD: Mini-Batch Gradient Descent)と呼ばれる方法が用いられます。この方法では、データセットが、\(K\) のサンプルを含む等しいサイズの \(N\) 個の小さなバッチへと、ランダムに分割されます。\(K\) は小さな正の数でも良いし、数十から数百にすることもできます。この数は特定のアーキテクチャとアプリケーションごとに異なります。\(K=1\) の場合はSDG、\(K\) がデータセット全体のサイズの場合はバッチ勾配降下法になります。紛らわしいことに、人によっては「SGD」をMB-GDとサンプルを1つづつ評価する方法、両方の意味で使うこともあるので気をつけてください。
MB-GDによって両方の長所を手に入れることができました。勾配はSGDよりも滑らかで安定し、バッチ勾配降下法とかなり似てはいますが、更新ごとにデータセットのすべてのサンプルを評価しなくて良いため大幅なスピードアップができます。更にMB-GDは並列化可能な行列演算によって非常に効率的に計算できます。
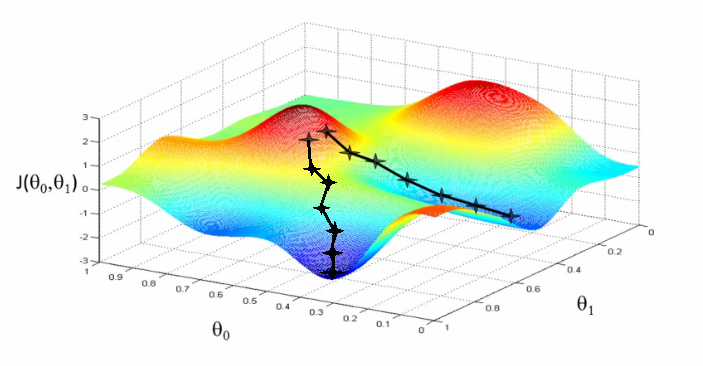
実際にMB-GDとSGDは、ニューラルネットワークの損失関数を効率的に最適化する上でうまく機能します。しかし難点もあります。
- 前述した鞍点の問題。損失関数が平坦で勾配が0に非常に近くなるパラメータをもつ場合に行き詰まってしまうことがあります。
- 学習率はハイパーパラメータとして手動で設定する必要がありますが、これは簡単ではありません。学習率が低すぎると収束が遅くなり、高すぎると正しい経路を通り越す可能性があります。
モーメンタム法
モーメンタム法は勾配降下法のうち、重みの更新に慣性を用いる種類を指します。言い換えると、重みはもはや現在の時刻における勾配だけの関数ではなく、過去の更新レートを元に徐々に調整されるのです。
標準的な勾配降下法では、勾配 \(\nabla J(W)\) を計算し、学習率 \(\alpha\) を含む下記のパラメータ更新式を用いました。
\[W_{t} := W_{t} - \alpha \nabla J(W_{t})\]現在の時刻を示すために、以前は省略されていた添え字 \(t\) を追加したことに注目してください。それに対して、モーメンタム法を用いた勾配降下法の一般的な式は次のように表されます。
\[z_{t} := \beta z_{t-1} + \nabla J(W_{t-1})\] \[W_{t} := W_{t-1} - \alpha z_{t}\]パラメータ更新式の勾配 \(\nabla J(W_{t})\) を過去の時刻の勾配を考慮したより複雑な関数\(z_{t}\) で置き換えました。\(\beta\) が大きいほど、パラメータ更新のモーメンタムは大きくなります。\(\beta = 0\) とすると、通常の勾配降下法になります。 \(\alpha\) は以前と同じくプロセス全体の学習率を制御します。
更新の道筋は坂を下るボールのように考えることができます。勾配が大きく変化する場所にボールがさしかかっても、勢いがあるため勾配に沿って少しずつ向きを変えるだけでほぼ同じ方向に進み続けます。モーメンタム法は過去の更新から積み重ねたスピードに乗って鞍点や極小値から抜け出す助けにもなります。また、損失関数の曲面が局地的に一定の向きにだけ大きく傾いている場所ではジグザクな蛇行がしばしば問題になりますが、勢いがあることでこの問題にも対抗できます。
上に示した標準的なモーメンタム法の式の代わりの1つに、次に示すネステロフ加速勾配降下法があります。
\[z_{t} := \beta z_{t-1} + \nabla J(W_{t-1} - \beta z_{t-1} )\]ただ1つ違う点は現在の位置での勾配(\(W_{t-1}\))を評価するのではなく、その時点での勢いを考慮した次の時刻(\(W_{t-1} - \beta z_{t-1}\))でのおおよその位置を評価に用いることです。今の場所ではなく、行き先の勾配を計算することで損失関数の曲面を予測し、モーメント項をよりうまく調整することができます。下の図を見てください。
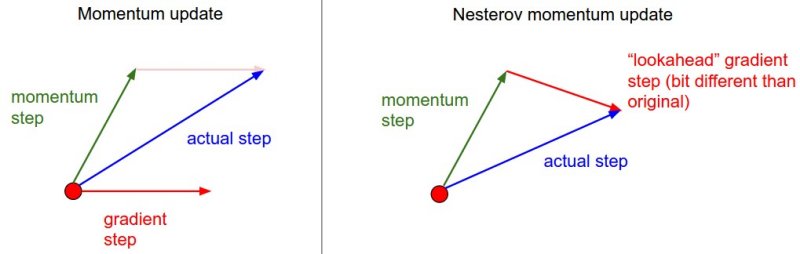
モーメンタム法はとてもうまく働きますが、パラメータ間内部の非対称性にもかかわらず勾配全体に対して単一の式を用いるのはMB-GDやSGDと同様です。これに対して次の節で説明する、勾配の各要素に対して適応する手法にはいくつかの利点があります。distill.pubの記事では、モーメンタム法についてより深く数学的に解説し、なぜ動作するのかをわかり易く説明しています。
適応的手法
モーメンタム法には多くの種類があります。一般に、勾配降下でのパラメータを更新するための速く効率的で正確な戦略を見つけることがこの分野の科学研究の主な目的ですが、それらについての徹底した議論は本書の範囲外です。代わりにこの節では実際の実装で良く見られるいくつかの種類について簡単にまとめ、より包括的な解説はオンラインのリソースに任せることにします。
訓練の方法で悩ましい問題の1つは学習率 \(\alpha\) の設定です。一般的に、\(\alpha\) にはまず初期値を設定し、幾らかの時刻を通じて徐々に減衰させてより正確に良い解へと収束させます。\(\alpha\) はそれぞれのパラメータに対して同じ値が用いられます。
この方法は、時刻ごとの損失表面の特性にかかわらず、個々のパラメータについて学習率が全く同じスケジュールに従うと仮定している点で不満が残ります。加えてそもそも、\(\alpha\) とその減衰率を設定する方法が不明確です。素の勾配下降法の「ワンサイズ・フィット・オール」なアプローチとは違い、モーメンタム法とネステロフ勾配下降法ではある程度局所的な状況に基づいて更新レートを決めるので、この問題を軽減するのに役立ちます。それでも、 \(\alpha\) の選択とパラメータ間の柔軟性のなさは問題です。
いくつかの手法ではこの欠点に対処するため、損失には全てのパラメータにわたり大きな分散があるという仮定に基き、学習率を各パラメータごとに個別に適応させます。パラメータごとに更新を行う最も簡単な手法は、AdaGrad(適応型劣勾配「Adaptive subGradient」の略)です。AdaGradでもパラメータは各々の勾配に応じて更新されますが、新たに導入された係数が、勾配が大きくなりやすいパラメータと小さくなりやすいパラメータとの間で学習の速さを等しくするように働きます。AdaGradは次の式で定義されます(添え字 $i$ はこれまでのように時刻ではなく重みのインデックスを示すので、混乱しないよう注意してください)。
\[w_{i} := w_{i} - \frac{\alpha}{\sqrt{G_{i}+\epsilon}} \frac{\partial J}{\partial w_{i}}\]\(\sqrt{G_{i}+\epsilon}\) は訓練を開始してからの各時刻におけるパラメータの勾配の二乗の和を表します(\(\epsilon\) 項には、ゼロ除算を避けるために十分小さな数、例えば \(10^{-8}\) を用います)。各パラメータについて \(\alpha\) をその数で除算することで、それまで大きな勾配にあったパラメータの学習率を実質的に低下させ、逆に勾配が小さいかほとんどない場合はパラメータの学習を早めます。
AdaGradは初期の学習率 \(\alpha\) をハイパーパラメータとして扱う必要性をほぼ排除しますが、固有の課題もあります。 AdaGradの典型的な問題は、時間が経つにつれパラメータごとに \(G_{i}\) が累積し、更新の量が小さくなることで途中で学習が止まってしまうことです。AdaGradの変形であるAdaDeltaは、勾配累積項の範囲を最後のいくつかの更新に制限することによって効果的にこの問題に対処しています。AdaDeltaと非常によく似たもう1つの適応方法はRMSpropです。 RMSpropはCourseraの講義でGeoffrey Hintonによって提案されましたが論文は出版されていません。この手法では標準的なイージング式と減衰率を用いることで、よりシンプルに過去の更新の二乗和の影響を制限します(ここで減衰率はハイパーパラメータになります)。したがって、AdaDeltaとRMSpropでは、訓練が終了するまで学習率が単調に減衰するのではなく、更新の速さはパラメータだけでなく時間にも基づいて適応します。
Adamと更新方法の比較
本章で最後に説明するのは最新の手法の1つ、Adamで、この名前は適応モーメント推定(adaptive moment estimation)に由来しています。Adamは、適応的手法とモーメンタム法の両方の利点を持っています。AdaDeltaやRMSpropと同様に、Adamは過去の勾配のスライディングウィンドウに基づいて学習率をパラメータごとに調整しますが、時刻に沿って道筋を滑らかにするためのモーメンタムの成分もあります。
訳注:スライディングウィンドウとは時系列のデータ(ここでは過去の勾配)について、ある決められた大きさの窓(ウィンドウ)に含まれるデータのみ取り扱うこと。名称は窓を時刻ごとにずらす(スライドする)ことから。
さらに多くの手法が存在しますが、それらの徹底した議論は本章の範囲外です。派生形や実用的なヒントを含めたより包括的な議論は、Sebastian Ruderのブログ記事を参照してください。
この素晴らしいビジュアライゼーションはAlec Radfordによるもので、今まで説明したさまざまな勾配の更新方法の特徴的な振る舞いを示しています。モーメンタム法とネステロフ加速勾配降下法(NAG)は「下り坂を転がる」速度が付きすぎて最適な経路をオーバーシュートする傾向があることに対し、標準的なSGDは適切な経路を取るものの遅すぎることに注意してください。適応的手法であるAdaGrad、AdaDelta、RMSProp(Adamもここに含まれます)はパラメータごとの柔軟性があることで、これらの問題を回避する傾向があります。
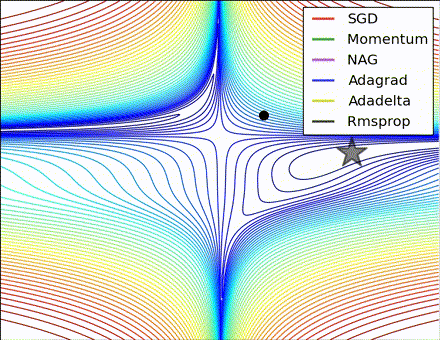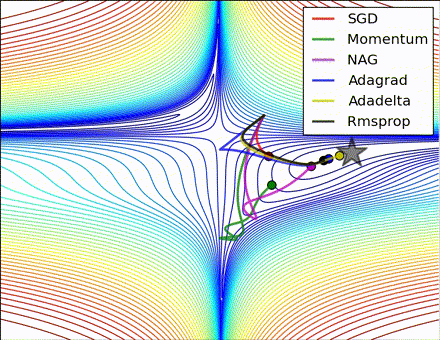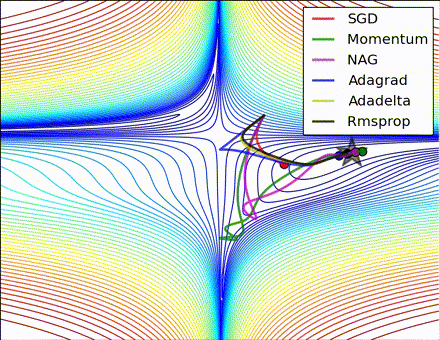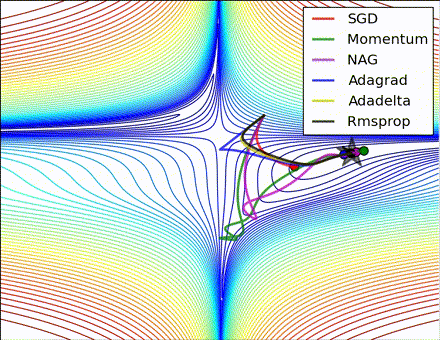
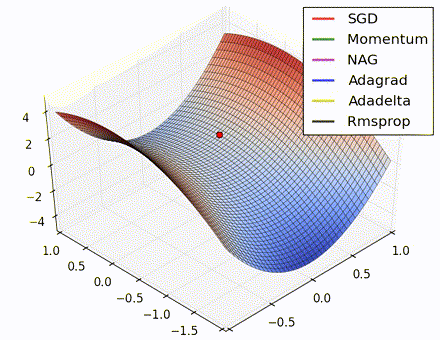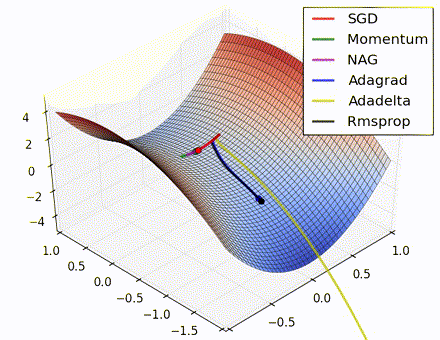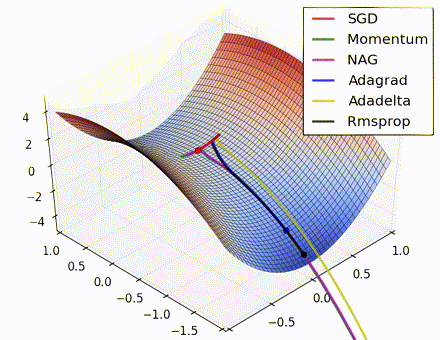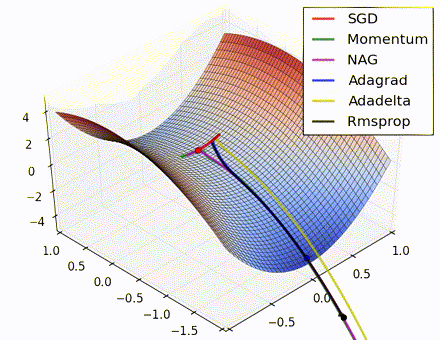
それではどの最適化手法が最適なのでしょうか。簡単な答えはなく、データの特性やその他の訓練の制約と考慮事項に大きく依存します。ですが、少なくとも手始めとするにはAdamが有望株です。データがまばらであるか不均等に分布している場合、純粋な適応手法が最も効果的です。それぞれの手法をどの場合に使うかについての徹底した議論は本章の範囲を超えていますので、最適化に関する学術論文、またはYoshua Bengioの実用的な要約などを参照してください。
勾配降下法の最適化の詳細は下記の文献を参照してください。
ハイパーパラメータとその評価
ネットワークのパラメータの最適化について理解したので、手順の全体をまとめることができます。最終的なモデルを訓練する素朴な方法は、全てのデータに対して勾配降下法を実行することです。しかしこれを行うと問題に突き当たります。どのようにモデルの精度を評価すれば良いのでしょう。すべてのラベル付きデータを訓練で使い果たしてしまったので、評価を行うにはモデルをトレーニングセットで再度実行し、出力と正解データ(与えられたラベル)の違いを測定するしかありません。この方法がなぜ良くないのかを理解するためには、過学習という現象を理解する必要があります。
過学習
過学習とは、モデルがトレーニングセットを正確に予測するように最適化され過ぎてしまい、(学習の本来の目的である)未知のデータに対応する汎用性が失われてしまっている状態のことを指します。これはモデルが、トレーニングセットに含まれるノイズまで拾って、データに完全に沿うように大きくねじ曲がってしまった場合にも起こります。
過学習とは、アルゴリズムがある種のインチキをしているのだと考えることもできます。知っているデータに対してだけ誤差が最小限になるようにして、見せ掛けだけの高得点を出せるとあなたを信じ込ませようとしているのです。これはファッションの仕組みを学ぼうとしているのに、70年代のディスコにいる人々の写真しか見たことがなくて、ベルボトム、デニムジャケット、厚底の靴が全てだと思っているようなものです。親しい友達や家族にもそんな人がいるかもしれませんね。
下のグラフで例を見ることができます。黒い点で示された11個のサンプルに対して適合するように、2つの関数を訓練します。1つは直線で、大まかにデータの特徴を捉えています。もう1つはとても曲がりくねった線で、全てのサンプルに完璧に一致しています。一見、後者の方が誤差が少ない(実際に0です)ので、トレーニングデータに対して良く適合しているように思えるかもしれません。しかしそれは潜在的なばらつきをうまく捉えることができておらず、未知のデータに対しては残念な性能しか出せないでしょう。
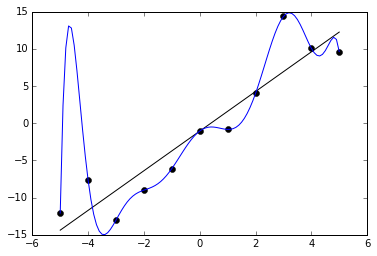
どのようにすれば過学習を避けられるでしょうか。最も簡単な解決策は、データセットをトレーニングセットとテストセットに分割することです。トレーニングセットは、これまでに説明した最適化の手順で使いますが、訓練されたモデルの精度はテストセットを使って評価します。テストセットはトレーニングセットから分けられているので、モデルがインチキする、つまり後でテストに使われるサンプルを暗記してしまうのを防ぐことができます。訓練をする間、トレーニングセットとテストセットに対する精度をチェックします。長い時間訓練を行うほどトレーニングセットに対する精度は上がり続けますが、テストセットに対する精度は改善しなくなるでしょう。これは訓練を打ち切る合図です。一般にトレーニングセットに対する精度はテストセットに対する精度よりも高くなると考えられますが、あまり高すぎる値は過学習を起こしていることを示唆しています。
交差検証とハイパーパラメータの選択
上記の手順は過学習と戦う良い手始めになりますが、それだけでは不十分です。最適化を始める前に決めなくてはいけない重要なことがいくつかあります。どんなモデル構造を使うべきでしょうか。いくつの層と隠れたニューロンが必要でしょうか。学習率とその他のハイパーパラメータはどのように設定するべきでしょうか。単純に違う設定を試して、テストセットに対して最も良い結果を出すものを選ぶこともできます。しかし問題はこれらのハイパーパラメータを特定のテストセットだけに最適化し、任意のデータや未知のデータに適応できなくなってしまう危険があるということです。これもまた過剰な適応を行ってしまっていることになります。
これを解決するにはデータを2つではなく、トレーニングセット、検証セット、テストセットの3つに分ける方法があります。通常、データ全体の70%か80%がトレーニングセットに割かれ、残りが均等に検証セットとテストセットに分けられます。トレーニングセットを使って訓練を行い、検証セットを使って評価をして、最適なハイパーパラメータを求め、またいつ訓練を止めれば良いか(通常、検証セットに対しての精度が改善しなくなった時)を知ります。交差検証という手法がより望ましい場合もあります。トレーニングセットと検証セットは合わせていくつかの(例えば10個)等しいサイズに分けられ、それぞれの分割された部分が順番に検証セットとして用いられます。ひとつの検証セットが継続的に使われることもあります。検証の後、ずっと残して置いたテストセットを用いて最後の評価をおこないます。
訳注:交差検証ではトレーニングセットと検証セットを別々に用意するのではなく、同じデータセットを分割したものを交代で用います。例えば10個に分けたセットそれぞれに1〜10と番号を付けた場合、まず2〜10でトレーニングを行い、1で検証、次は1、3〜10でトレーニング、2で検証、というように順番に役割を交代させます。
最近では、多くの研究者が訓練プロセス自体の中でモデルの構造とハイパーパラメータを学習する方法を工夫し始めています。Google Brainの研究者はこれをAuto MLと呼んでいます。このような手法は機械学習において、未だに人間の手を必要とする退屈な部分を自動化する大きな可能性を秘めており、おそらくは誰かが問題を定義してデータセットを提供するだけで機械学習が行えるような未来を指し示しています。
正則化
正則化とは、過学習を防止するため、または好ましくない状態が起こりにくくするために、ニューラルネットワークに制約を課すことを指します。 過学習が起こるケースの1つに、重みが大きくなりすぎる場合があります。この時、上記の例で見たように関数がトレーニングセットに含まれたノイズを拾って大きくカーブしてしまうことがあります。
正則化を行う方法の1つは、損失関数に手を加えて大きな重みに対してペナルティを与えるような項を追加することです。ニューラルネットワークを \(f\) としたとき、最適化する損失関数は下記の平均二乗誤差で表されます。
\[J = \frac{1}{n} \sum_i{(y_i - f(x_i))^2}\]下記のL2正則化項 $R(f)$ を損失関数に付け加えると、大きな重みに対してペナルティを与えることができます。
\[R(f) = \frac{1}{2} \lambda \sum{w^2}\]この項は単純に、全ての重みの二乗の和に、正則化項全体の大きさ(つまり影響力)を調整する新しいハイパーパラメータ $\lambda$を掛けたものです。係数の $\frac{1}{2}$ は単に微分した場合に便利なように付いています。これをもともとの損失関数に加えると下記のようになります。
\[J = \frac{1}{n} \sum_i{(y_i - f(x_i))^2} + R(f)\]この正則化項は、先ほどのように大きな重みを積み重ねてひどく曲がりくねることのないようなパラメータを、勾配降下法が見つける助けになります。
この他にも、L1距離または「マンハッタン距離」を用いたものなど、異なる種類の正則化項があります。これらは微妙に異なる特性を持ちますが効果としてはほぼ同じです。
ドロップアウト
ドロップアウトは2014年にNitish Srivastavaらによって導入された正則化のための巧妙なテクニックです。訓練を行う際にドロップアウトがある層に対して適用されると、接続されたニューロンのうち一定の割合(これはハイパーパラメータで一般的には20%から50%に設定されます)を無効化(ドロップアウト)します。ドロップアウトするニューロンは、訓練の間ランダムに入れ替えられます。ニューロンが必ずそこにあるとは限らなくなるため、結果としてネットワークがいくつかのニューロンに極端に依存する傾向を減らすことができます。これはネットワークがよりバランスのとれた表現を学ぶよう矯正し、過学習を防ぎます。下記はオリジナルの論文からの図解です。
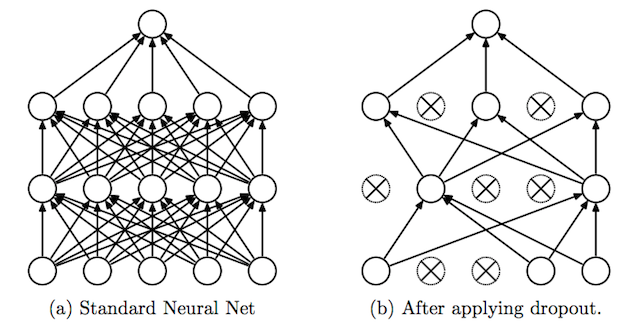
もう1つ、正則化の変わった方法には入力に少しのノイズを加えるやり方があります。この他にも沢山の方法が提案されていますがその効果はまちまちであり、ここでは詳しく説明しません。
バックプロパゲーション
ここまで、ニューラルネットワークのパラメータを決定するための勾配降下アルゴリズムと、それをアレンジした適応的手法、またモーメンタム法などをいくつか紹介しました。どの手法を選択しても、ネットワークの重みおよびバイアスに対する損失関数の勾配を計算する必要があります。これは簡単な作業ではありません。なぜかを知るために、どうやってこれを求めるのかについて考えてみましょう。
標準的な勾配降下法の重みの更新は、次の式で与えられることを思い出してください。
\[W_{t} := W_{t} - \alpha \nabla J(W_{t})\]$\nabla J(W_{t})$ が損失の勾配です。これまでに見てきたどの勾配降下法のバリエーションにおいてもこの値を何らかの形で計算しなければなりません。勾配は、各パラメータに対する損失関数の偏微分の各々を含むベクトルであり、以下のように与えられることを思い出してください(簡略化のため $t$ は省略)。
\[\nabla J(W) = \Biggl(\frac{\partial J}{\partial w_1}, \frac{\partial J}{\partial w_2}, \cdots, \frac{\partial J}{\partial w_N} \Biggr)\]では、どのようにそれぞれの $\frac{\partial J}{\partial w_i}$ を計算するのでしょうか。最も明らかな方法は、通常の微積分の微分方程式を用いて計算することです。
\[\frac{\partial J}{\partial w_i} \approx \frac{J(W + \epsilon e_i) - J(W)}{\epsilon}\]$e_i$ はone-hotベクトル($i$ 番目の要素は1でそれ以外は0であるベクトル)であり、 $\epsilon$ は十分小さな数です。これは理論上はうまくいきますが、収束の速度の面で大きな問題があります。勾配の要素の1つを得るには、$W + \epsilon e_i$ と $W$ の両方において損失関数を計算する必要があります。$W$ については一度計算すれば良いですが、$J(W + \epsilon e_i)$ は $w_i$ 全てに対して計算が必要です。典型的なディープニューラルネットワークは、何百万から数億の重みを持っています。一回の重みの更新のために数百万回のフォワードパスが必要であり、それぞれのフォワードパスは数百万回の操作を伴います。これでは、ニューラルネットワークの訓練には全く実用的ではありません。
それではどのように重みを求めるのでしょうか。事実これは、バックプロパゲーションが開発されるまでニューラルネットワークの訓練の大きな障害となっていました。誰がバックプロパゲーション(英語では「バックプロップ」と略記します)を発明したのかは論争の的になっており、多くの人々が歴史の中で別々の時期に再発明したり、様々な問題に適用される同様の概念を見つけたようです。バックプロパゲーションは、主にニューラルネットワークに関連付けられるものの、連続的微分可能な多変数関数の勾配の計算が含まれるあらゆる問題に使用することができます。そのため、その開発はニューラルネットワークの発展とはある程度並行して行われました。2014年にはJürgen Schmidhuberがバックプロパゲーションの開発の背景にある関連研究のレビューをまとめています。
バックプロパゲーションは、David Rumelhart、Geoffrey Hinton、Ronald J. Williamsによる1986年の画期的な論文の中で初めて、勾配降下法によりニューラルネットワークを最適化するタスクに用いられました。その後の研究は80年代と90年代に、最初に畳み込みネットワークに適用したYann LeCunによって行われました。ニューラルネットワークの成功は彼らとそのチームの努力によるところが大きいのです。
バックプロパゲーションの仕組みを全て説明するのは本書の範囲外です。その代わりに、この段落ではバックプロパゲーションに何ができるのかについて、基本的で大まかな考え方を説明し、技術的な説明はいくつかの参考文献に任せます。基本的な考えでは、バックプロパゲーションを用いると、単純な手法のようにパラメータごとに1つのフォワードパスを実行するのではなく、ネットワークのフォワードパスとバックワードパスで勾配のすべての要素を計算することができるようになります。これは微積分の連鎖率を利用することで可能になります。連鎖律を用いると、微分を個々の関数部分の積に分解できます。すべての接続に沿ったフォワードパスの差分を追跡、記録することで、フォワードパスの最後に損失項を求め、それを層ごとに「逆方向に誤差を伝播」して勾配を計算できます。これにより、バックワードパスはフォワードパスとほぼ同じ計算量で済むため訓練は劇的に加速し、ディープニューラルネットワークの勾配降下法は解決可能な問題になります。
バックプロパゲーションの導出方法についての詳しい技術的説明は下記のリンクを参照してください。
山を下りていく
本章をここまでを読んだ皆さんは、本章の冒頭に登場する登山者のアナロジーの意味が分かってきたことでしょう。そうであれば、おめでとうございます。ニューラルネットワークがどのようにして訓練されるかについて理論と実践を十分に理解したので、この分野の実際の科学研究がより親しみすく思えるでしょう。何年もの間、多くの科学者は、バックプロパゲーションに対する多様かつ風変りな拡張を提案してきました。Geoffrey Hinton自身を含む他の研究者らは、機械学習はバックプロパゲーションから先へ進み、やり直さなければならないと提案しています。しかし本書の執筆時点では、バックプロパゲーションによる勾配降下法は、ニューラルネットワークやその他の多くの機械学習モデルの訓練の最も有力なパラダイムであり続け、しばらくの間はその道を歩み続けるように見えます。
続くいくつかの章では、より進んだトピックについて見ていきます。次の章では、畳み込みニューラルネットワークや特に本書の核であるアートやクリエイティブな目的への応用について紹介します。